難易度
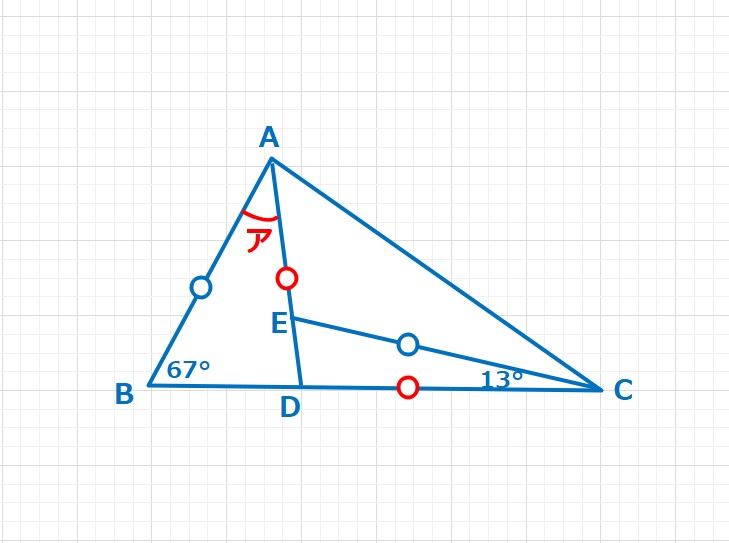
【問題】∠ABC=67°である三角形ABCがあります。今、BC上にAD=DCとなるような点Dをとり、またCE=AB,∠ECB=13°となるような点EをAD上にとったとき、ア=∠BADは何度ですか。
【ヒント】
与えられた情報が多めですし、離れた2辺の長さが等しい三角形問題の定番のアプローチ方法からせめていくと解法が見えてくると思います。AD=CDを活用し、△ABD(黄緑)を△CDF(黄緑)に移動させます。その際、∠ADB=∠CDFなので、∠ADB+∠ADC=180°=∠ADC+∠CDFとなりますのでADFは一直線となります。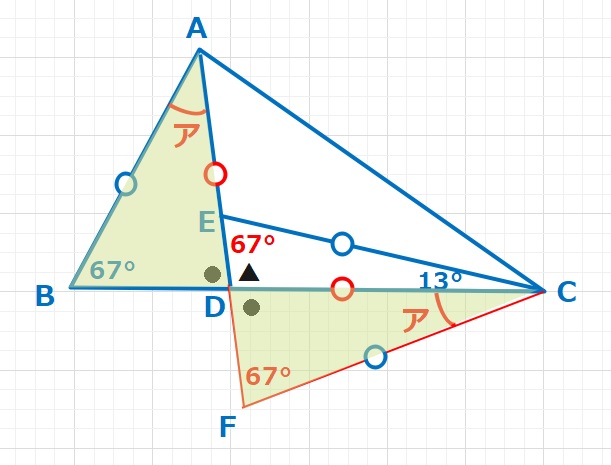
【解答】EDFは一直線なので、CEFは三角形となります。またCE=CFなので、△CEFは二等辺三角形となります。よって、∠CFE=∠ABD=67°=∠CEFとなり、∠ECF=180-(67+67)=180-134=46°
よってア=∠DCF=46-13=33°・・・(答え)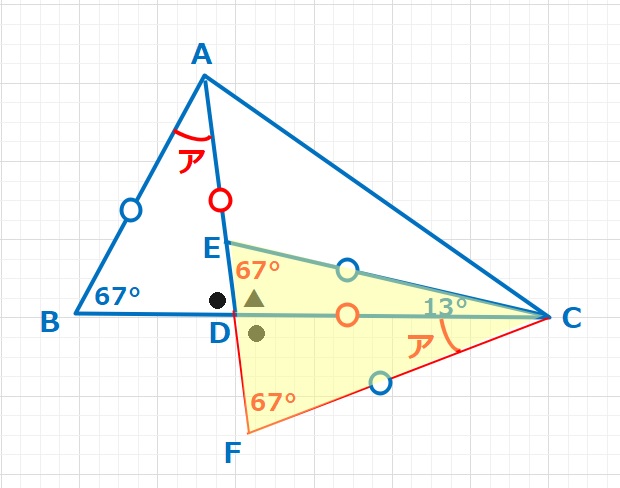
コメント