三角形の内角の和は180°
なぜか理由を少し考えてみましょう。
下図のように三角形ABCがあるとき、点Aを通りBCに平行な線、DEを引いてみます。
対頂角とさっ角・同位角の関係を使うと、図の●はすべて等しくなります。
同様に図の●もすべて等しくなります。
青と赤と黄色の●は、一直線に集めることができるので、内角の和は180°となります。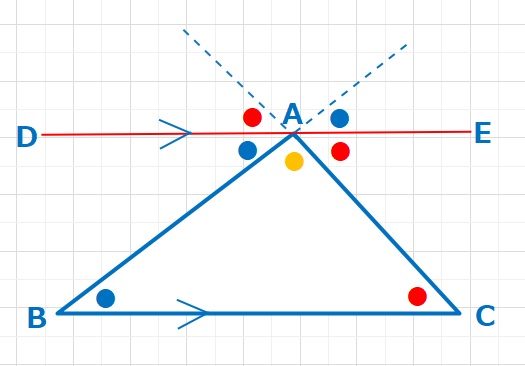
多角形の内角の和
多角形の内角の和は下図のようになります。
下図をしっかり眺めていると、規則性が見えてきませんか?
3角形の内角の和は上で説明したとおり、180°です。
そこから、4,5,6,7と角が1つずつ増えてますね。それと合わせて180°,360°,540°・・
と180°ずつ増えていっています。
暗記してしまうのもよいですが、いざという時に自分で導ける方がよいので規則性を
自分で考えてみましょう。
3角形,180° から始まって、12角形,1800°と角度が10倍になっています。
それでは 「〇角形の内角の和」は何度でしょうか?
12角形で180°の10倍なので、〇角形は180°×(〇-2)となることがわかるでしょう。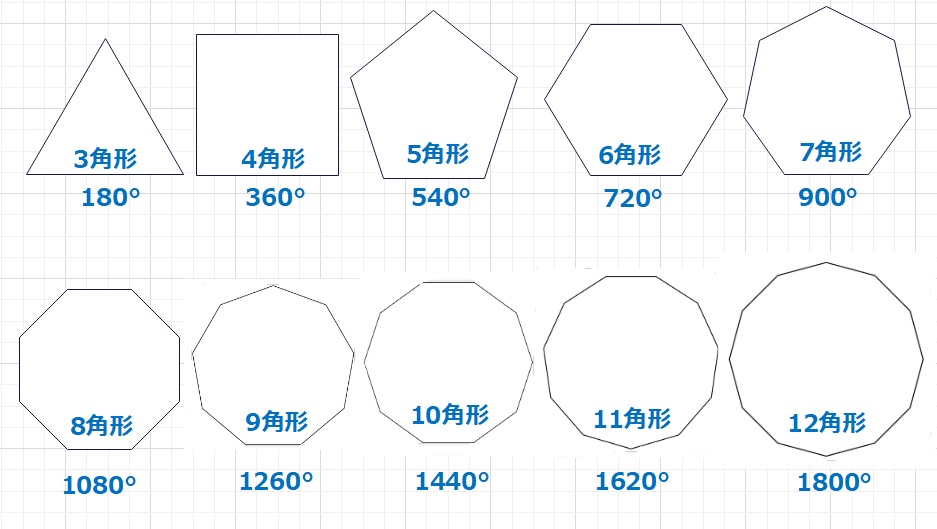
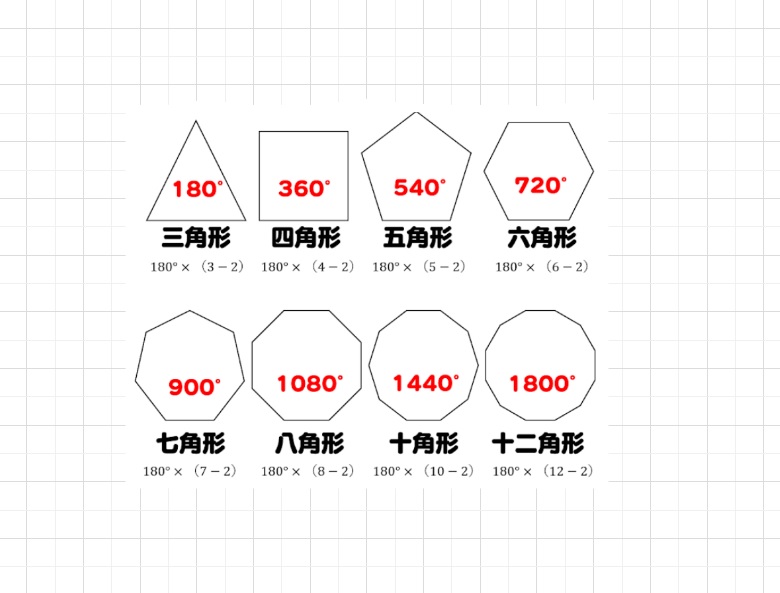
〇角形の内角の和=180×(〇-2)
なぜ、〇角形の内角の和=180×(〇ー2)になるのでしょうか。
下図をじっくり見てください。
多角形を3角形に分割します。4角形は2つの三角形に、5角形は3つの三角形に、
6角形は4つの三角形に分割できます。これから〇角形は〇ー2個の三角形に分割できます。
1つの3角形の内角の和は180°なので、〇角形の内角の和は180×(〇ー2)となります。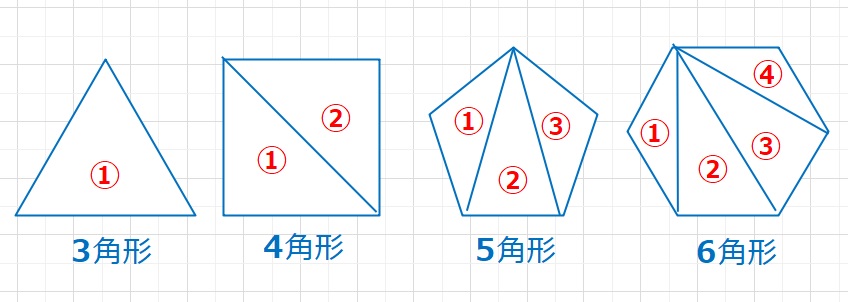
コメント