正六角形を中心として、面積を求める問題をよく見かけます。
正六角形が出題されたときの対応方法を考えてみます。
以前ご紹介した通り、正六角形の6等分の方法として、下図の2パターンが
基本パターンとなります。
正六角形を中心とした面積を求めるときに武器として、下の4つを使います。
基本パターン 4つの武器
①正六角形の \(\displaystyle\frac{1}{6}\)の正三角形。
②その応用として、正六角形の2辺を延長して \(\displaystyle\frac{1}{6}\)の正三角形をつくる。
③正六角形の \(\displaystyle\frac{1}{6}\)の二等辺三角形。
④正三角形と二等辺三角形を組み合わせた \(\displaystyle\frac{1}{3}\)の直角三角形。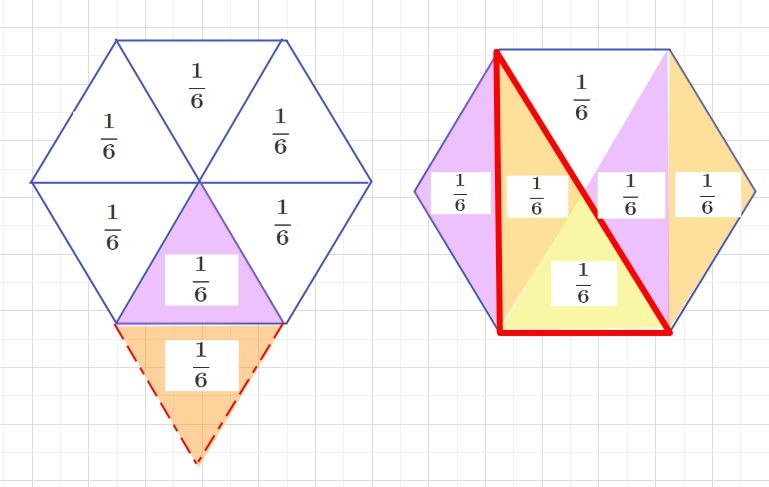
(おまけ)上図の変形パターンで下のような分割もあります。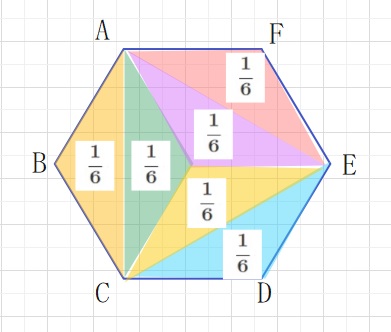
応用パターン 小さな正三角形と正六角形
応用パターンとして、下図のように分割すると、基本の正六角形の周りに
小さな正三角形ができます。先ほどの基本パターンの二等辺三角形の底辺に注目
すると、小さな正三角形の1辺の3つ分になっていることがわかります。
①基本パターンの二等辺三角形を3等分した、
正六角形の\(\displaystyle\frac{1}{6}\)×\(\displaystyle\frac{1}{3}\)となる
小さな二等辺三角形と正三角形 と活用する。
②小さな正六角形は
基本の正六角形から小さな正三角形と二等辺三角形合計12個を引いたものとなるため、
1-\(\displaystyle\frac{1}{6}\)×\(\displaystyle\frac{1}{3}\)×12
=1-\(\displaystyle\frac{2}{3}\)=\(\displaystyle\frac{1}{3}\)
つまり小さな正6角形はもとの正六角形の\(\displaystyle\frac{1}{3}\)となります。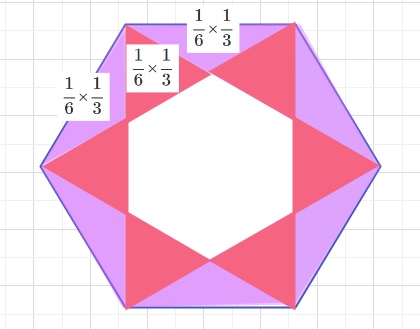
正六角形に内接する正三角形の面積(2021年開成中学入試出題)
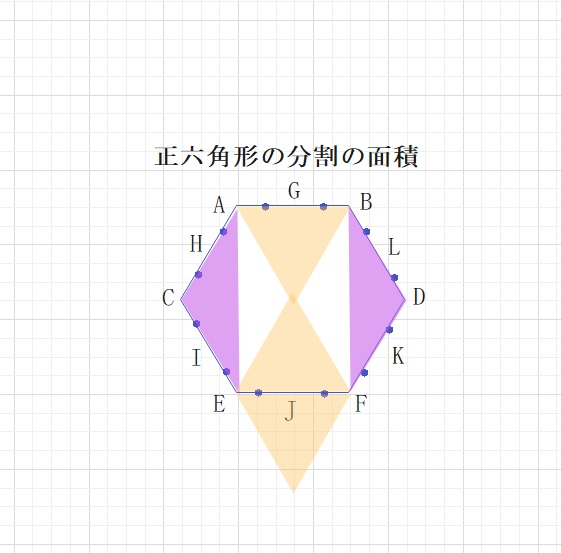
それではブルーの正三角形の面積はもとの正六角形のどれくらいでしょうか。
調べてみると全く同じテーマが2021年に開成中学で出題されてます。
下の図の基本のオレンジ色の正三角形をかつようすると、
AB:EF:CD=2:3:4 となります。
AB:CDは オレンジ色の正三角形の一辺をつかい2:4とすぐにわかります。
EF:CDは △GEFと△GCDが相似なので GF:GD=3:4=EF:CDとなります。
△G(A)(B):△GEFは GB:GF=2:3なので、面積の比は
2×2:4×4=4:9となります。
△GAB はもとの正六角形の\(\displaystyle\frac{1}{6}\)ですので
ブルーの正三角形=△GEF=\(\displaystyle\frac{1}{6}\)×9÷4となります。
△GEF=\(\displaystyle\frac{3}{2}\)×\(\displaystyle\frac{1}{4}\)=\(\displaystyle\frac{3}{8}\)
ブルーの正三角形はもとの正六角形の\(\displaystyle\frac{3}{8}\)とわかります。
逆に残りの3つの台形の面積部分は\(\displaystyle\frac{5}{8}\)となり、
1つあたりの台形の面積は\(\displaystyle\frac{5}{24}\)です。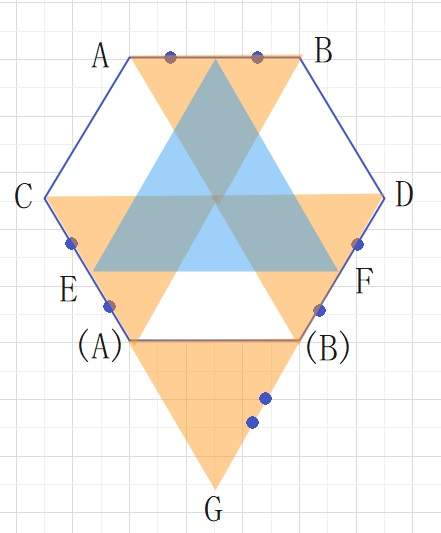
正六角形に内接する正六角形の面積
それでは下の緑の正六角形の面積はいくつでしょうか。
基本の二等辺三角形CAE と△CIHは相似な三角形で
CH:CA=1:2ですので △CIH:△CAE=1×1:2×2=1:4となります。
よって△CHIは△CAEの \(\displaystyle\frac{1}{4}\)となります。
△CHIはもとの正六角形の\(\displaystyle\frac{1}{6}\)×\(\displaystyle\frac{1}{4}\)となります
緑の正六角形は△CHI×6をもとの正六角形から引いたものですから
1-\(\displaystyle\frac{1}{4}\)=\(\displaystyle\frac{3}{4}\)となります。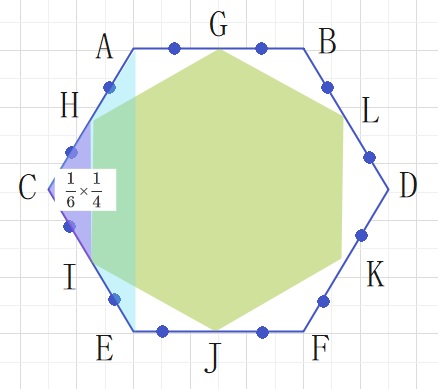
コメント