倍数の見分け方

２の倍数の見分け方

★１の位の数が偶数（０.2.4.6.8)ならば２の倍数

3の倍数・9の倍数の見分け方

★各位の和が３の倍数
★各位の和が９の倍数

７×１０００＋４×１００＋８×１０＋２
＝７×（９９９＋１）×４×（９９＋１）＋８×（９＋１）＋２
＝３×（３３３×７＋３３×４＋３×８）＋７＋４＋８＋２
前半部分は３の倍数、７＋４＋８＋２＝２１は３の倍数なので
「７４８２」は３の倍数です。

同様に、上の変形を
７×１０００＋４×１００＋８×１０＋２
＝７×（９９９＋１）×４×（９９＋１）＋８×（９＋１）＋２
＝9×（１１１×７＋１１×４＋１×８）＋７＋４＋８＋２
と分解すれば、前半部分が９の倍数ですので、７＋４＋８＋２が
9の倍数でしたら、9の倍数といえます。
ちなみに、「７４８２」は９の倍数ではないですね。

４の倍数の見分け方

★下２ケタの数が４の倍数か００

２×１０００＋８×１００＋０×１０＋０×１
＝２×（４×２５０）＋８×（４×２５）＋０×１０＋０×１
＝４×（２×２５０＋８×２５）＋０×１０＋０×１
となり、下２ケタ００となり「２８００」は４の倍数です。

５の倍数の見分け方

★下１ケタが５か０

6の倍数の見分け方

★2の倍数であり、かつ３の倍数。

７の倍数・１３の倍数の見分け方

正直これは、桁数が少ない時は実際に割った方が早いです。考え方として知っていると
応用できますので、ご紹介します
★①3桁ごとに区切った 数字を一つ飛ばしに足し、
　②その和の差が 7の倍数であれば、その数は7の倍数
★①3桁ごとに区切った 数字を一つ飛ばしに足し、
　②その和の差が 11の倍数であれば、その数は11の倍数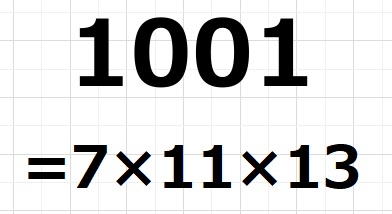

以前、１１の倍数の見分け方でご紹介しました　1001＝７×１１×１３を
活用します。
①②③④⑤⑥⑦⑧⑨という数字があるとします。
これを3ケタで区切ると、①②③/④⑤⑥/⑦⑧⑨となります。
①②③×1000000+④⑤⑥×1000+⑦⑧⑨と表現できます。
ここで、1000=(1001-1),1000000=1000×1000=(1001-1)×(1001-1)
=1001×1001－２×1001＋１と表現できます。
ここで１００１は7の倍数でもあり、11の倍数でもあり、13の倍数でもありますので、
①②③④⑤⑥⑦⑧⑨＝①②③×（7の倍数＋１）+④⑤⑥×(7の倍数-1)+⑦⑧⑨
=①②③×（13の倍数＋１）+④⑤⑥×(13の倍数-1)+⑦⑧⑨
そのため、　①②③＋⑦⑧⑨ー④⑤⑥　が7の倍数でしたら7の倍数
13の倍数でしたら13の倍数であることがわかります。

8の倍数の見分け方

★下3ケタが8の倍数
詳しくは別の機会にご紹介します。考え方としては１０００＝８×125を活用します。
　　　　
３４５６＝３×1000＋４56 となり、1000＝８×125ですので、
456が8の倍数でしたら8の倍数となります。
125の2倍は250、250の2倍は500、500の2倍は1000と２を3回かける（8倍する）
ことで1000を作るというのがミソです。
また、10000＝1000×10＝８×125×10ですので桁がふえても対応できます。