難易度(1.5)★☆☆☆☆
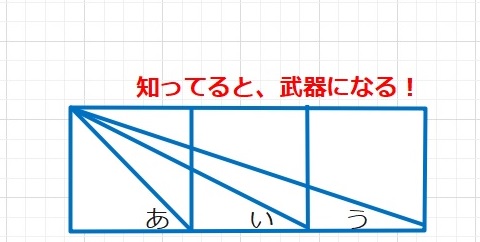
【問題】3つの正方形を横に並べた図形があります。あ,い,うの3つの角度の和は何度ですか。
【ヒント】
1:1の直角二等辺三角形の角度は、90°、45°、45°となりますから、「あ」の角度は45°となることはすぐにわかります。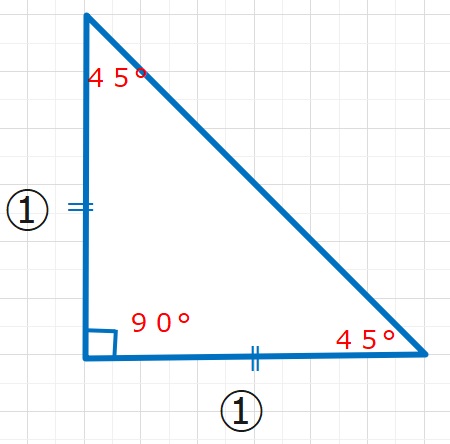
問題の図を下のように変形させます。
下の図で「い」と「え」の角度の合計は90°になり、少し大きめの1:1の直角二等辺三角形があらわれます。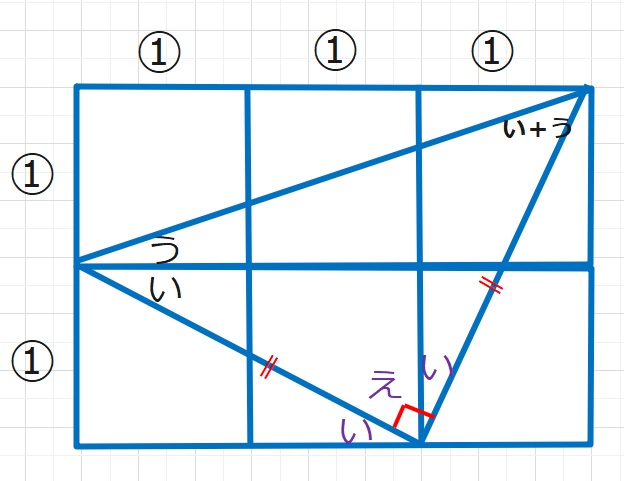
【解答】
「あ」は1:1の直角二等辺三角形より45°となる。
「い」+「う」も1:1の直角二等辺三角形より45°となる。
よって、「あ」+「い」+「う」=45+45=90° ・・・(答え)
三角形の性質について
定規セットを買うと、中に入っているのが、45,45,90の直角三角形の定規と、30,60,90の直角三角形の定規です。今は100円ショップでも売ってるので便利ですね。さて、なぜこれが便利なのか。下図を見てください。
基本図形として、正多角形というものがあります。正多角形とは「すべての辺の長さが等しく、すべての内角が等しい図形」のことを言います。なかでもよく見るものが、正方形(正四角形)と正三角形です。正方形を対角線で半分にした直角三角形と正三角形を図のように半分にした直角三角形が、45,45,90と30,60,90の直角三角形となります。
これが便利なところは、長さがわかれば、30°,45°,60°などの角度が自動的にわかるところです。
又逆も言えます、この角度がわかれば、同じ長さや、1:2の長さがわかるのです。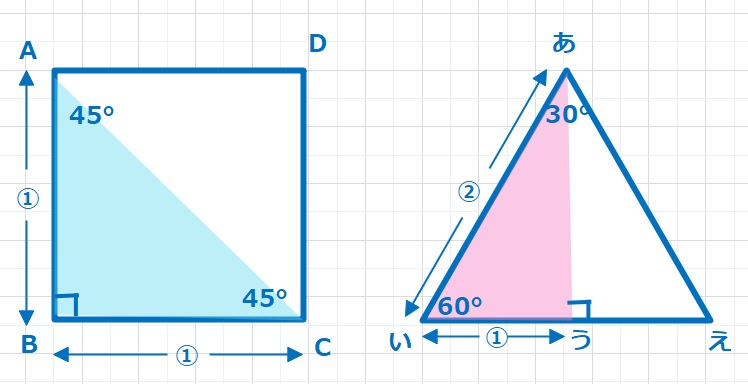
特殊な二等辺三角形
30°を頂角とした二等辺三角形(30,75,75の三角形)は下の右図のように回転すると、
わかりやすく、1つの辺の長さ(図の②の部分)がわかれば、高さがわかり、
面積を求めることができます。
その応用で、15,75,90の直角三角形も斜辺の長さがわかれば、
この図形を2つ組み合わせると30,75,75の二等辺三角形になるため、
面積を求めることができます。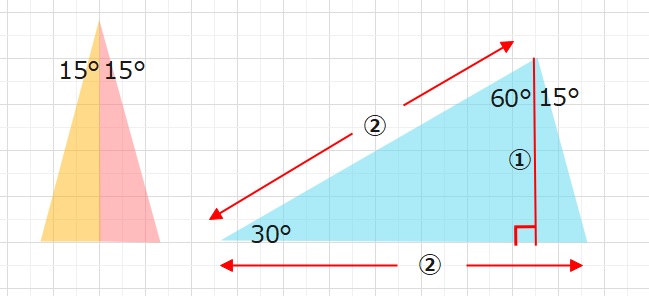
三角形の性質を使った応用(おうよう)
上の例のように、長さがわかれば自動的に角度がわかる、角度がわかれば自動的に長さがわかることはとても便利です。その応用が、したの(図1)ですが、1:2の直角三角形の「ア」と1:3の直角三角形の「イ」の角度を合計すると、「ア」+「イ」=45°となります。これ自体、知ってると得ですが、それよりも重要なのは、下の(図2)のように、なんでそうなるのか?とうことです。
このパズル的な考え方をみにつけることによって、考え方に幅(はば)がでてきます。
(図1)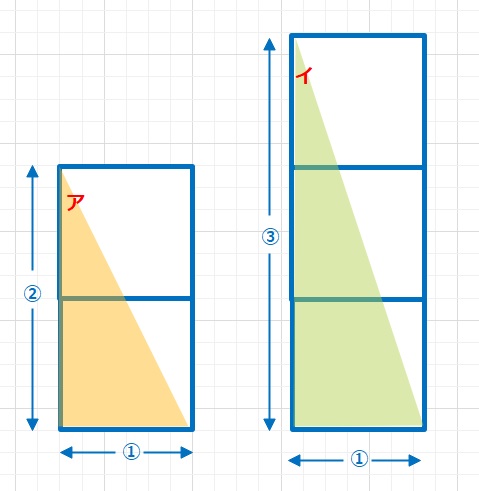
(図2)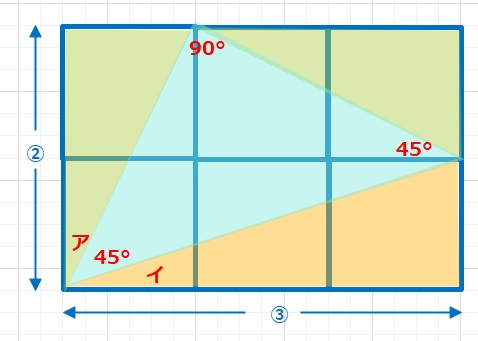
コメント