【問題】
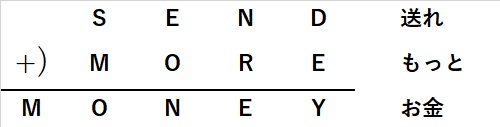
上のそれぞれのアルファベット、S,E,N,D・・・
には 0から9の数字が対応します。
どのアルファベットが何の数字に対応しているかを推理し、
計算式を完成させて下さい。
なお、Mは0をあてはめることはできず、
また右にかいてある日本語は問題を解くうえで
意味はありません。
【ヒント】
覆面算を解くうえでの準備は、どの数字を使ったかをチェックする
0~9の数字を書くことと、位どりの一、十、百・・・をかくこと
です。ここは、①②③④とか□□□とか、自分でわかればなんでもよい
と思います。
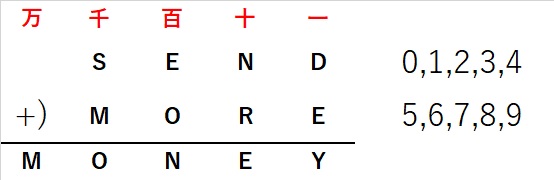
解けそうなところから解いていきます。
今回はMから解いていくのがよいでしょう。
算数的な思考を身につけるのにとても良い問題だと思います。
チャレンジしてみてください。
Mがわかれば次は、Oを確定してみましょう。
Oの次は、S、そしてRを確定してみましょう。
最後にE,N,D,Yを確定しましょう。
【解答】
SとMにあてはまる最も大きい数字をかんがえてみると、
9と8を選ぶことになるので、S+M=17となり
くり上がる数字は0か1しかありえません。
Mは0ではないと書いてますので、1で確定です。
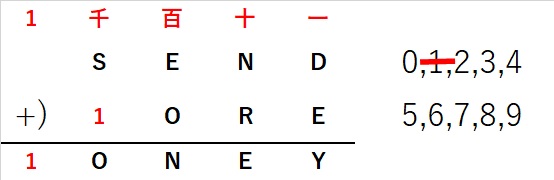
■次にOについて考えます。
千には、0か1の数字が入ります。
千=1のとき、千の位に注目して、1+S+1が
繰り上がる必要がありますので、Sは8か9となります。
S=8のとき1+8+1=10となり、O=0となります。
S=9のとき1+9+1=11となり、O=1となり
1はすでに使用ずみなので、成り立ちません。
千=0のとき、0+S+1がくり上がるためには
S=9となります。このときO=0となります。
以上より O=0が確定し、Sは8か9となります。
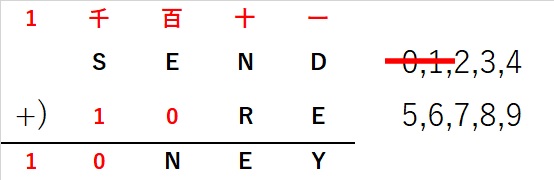
■つぎにSについて考えます。
Sは8か9なので、
S=8のとき、千=1となり、E+0はくり上がる
ことになり、Eは10以上となり、成り立ちません。
よってS=9とわかります。
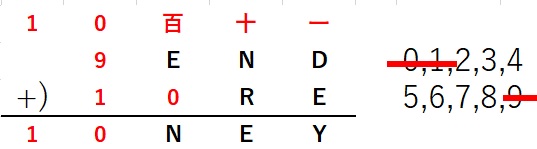
■つぎにRについて考えます。
E+百=N が成り立ちます。
また、十の位より、
十+N+R=十+E+百+R=E またはE+10
十+百+R=0 ・・・①
若しくは
十+百+R=10 ・・・②
十と百には0か1がはいりますので、
①が成り立つには、 十=0、百=0、R=0しかなく
0は既に使用してますので、成り立ちません。
②が成り立つには 十と百の組合せが、(0,0)(1,0)(0,1)(1,1)
のパターンがあり、そのときRはそれぞれ、10,9,9,8となります。
Rは一桁の数なので10ではなく、9はすでに使われてますので、
R=8とわかります。その時 (十,百)=(1,1)です。
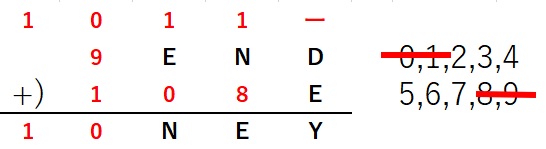
■E,N,D,Yについて考えます。
百の位から E+1=N また
使える数字は、2,3,4,5,6,7より
(E,N)=(2,3)(3,4)(4,5)(5,6)(6,7)となります。
一の位より D+E=Y+10
●E=2のとき Dは8、9となりますが既に使っているので
なりたちません。同様に、
●E=3のとき Dは7が候補となりますが、
D=7のときY=0となり0は既につかっているので
成り立ちません。
●E=4のとき D=6、7ですが、D=6のときは
Y=0、D=7のときはY=1と 0,1は既に使われて
いるので成り立ちません。
●E=5のとき D=5,6,7ですが、
同様にD=5,6はY=0,1となり成り立ちません。
E=5のとき D=7,Y=2,N=6で成り立ちます。
●E=6のときN=7となり D=4,5,6,7 が候補となります。
同様にDは6,7は使えずY=0,1となり成り立ちません。
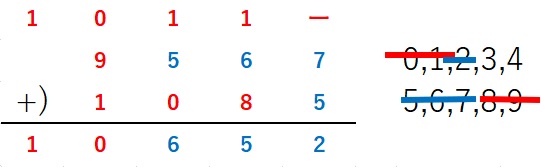
以上より E=5,N=6,D=7,Y=2とわかります。
よって最終の答えは、下の通りとなります。


コメント