難易度
本問題は四角形ではなく、三角形の内部に1点がある形となっていますが、ラングレーの問題-4点角問題(整角三角形の問題)に分類されます。外心や内心、傍心の性質について学んでいれば、若干難易度は下がりますが、小学生が解くとなると最高レベル、反則級クラスの問題といえると思います。
斉藤 浩 先生著の「ラングレーの問題にトドメをさす!」現代数学社 にも掲載されている問題です。この本によれば、この問題よりさらに難しい問題がまだまだあるようで、恐るべしです。
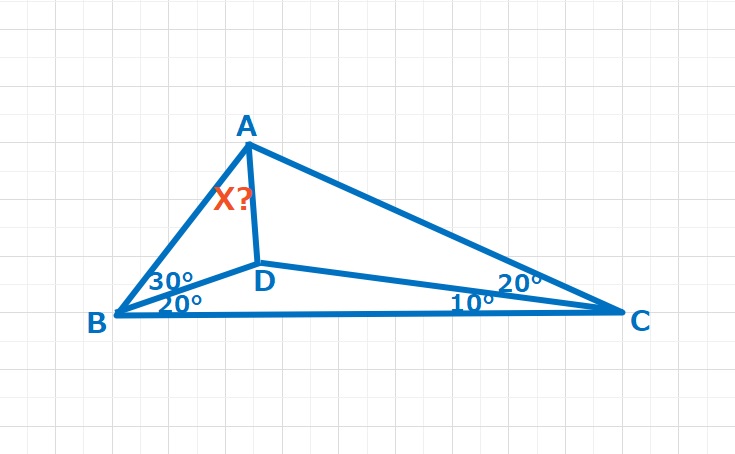
【ヒント】なんとか対称な図形を作ろうと工夫しますが、うまくいきません。まず点A,B,Cから
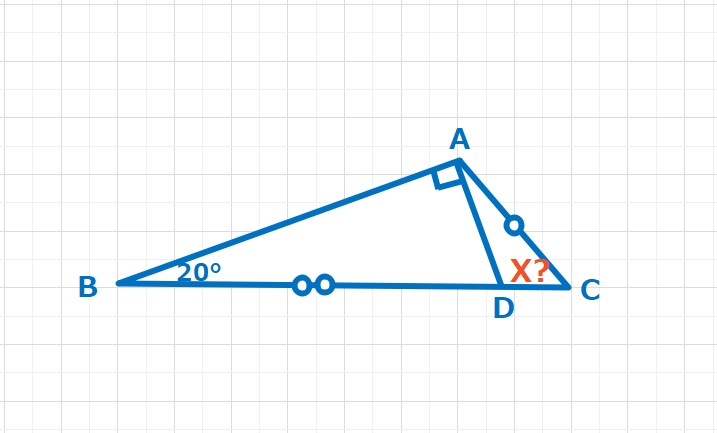
等距離にある点Eをとります。なんとなく△ABEは正三角形のような気がしますが、、、しっかりと検証が必要です。∠EBC=∠ECB=●とすると、△EAB,△EACは二等辺三角形なので∠EBA=●+50=∠EAB、∠ECA=●+30=∠CAE よって∠BAC=●●+80となります。
∠BEC=180-●● 以上より四角形ABECの内角の和=(●●●●+160)+180-●●=340+●●=360となります。 よって●=10°とわかります。
結果△ABEは正三角形でした!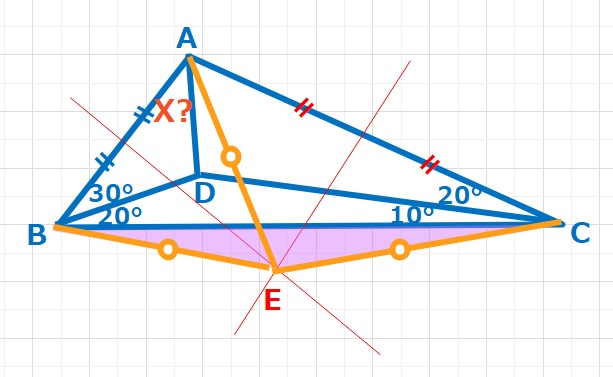
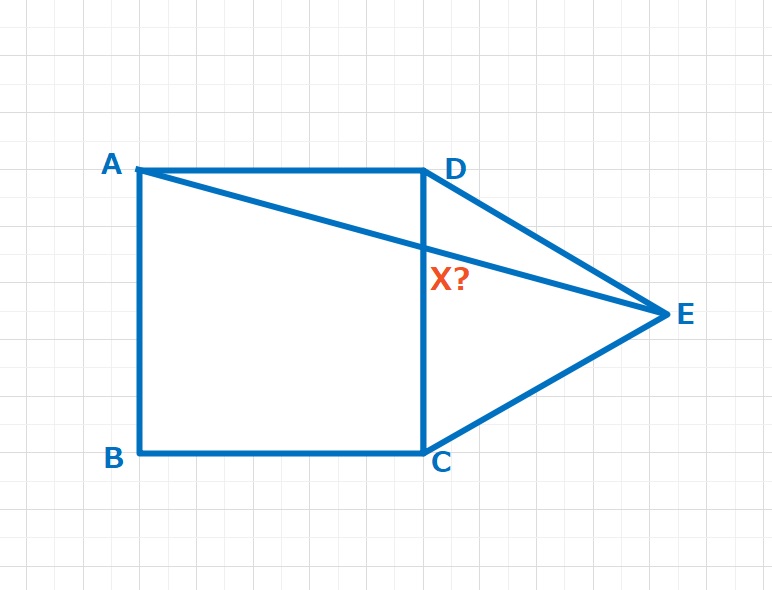
さて次に対称な図形を作るため、CEの延長とDBの延長の交点をFとすると、∠BEF=10+10=20°
∠BFE=30-20=10°となります。△BAFと△BEFは二辺(BA=BE,BF共通)とその間の角(∠ABF=∠EBF=150°)が等しいので合同な三角形で ∠BAF=20°です。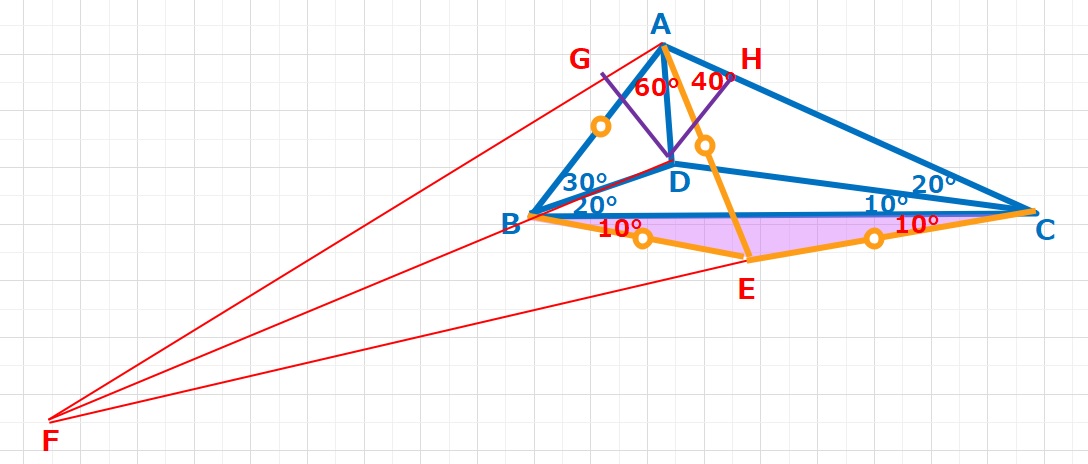
【解答】
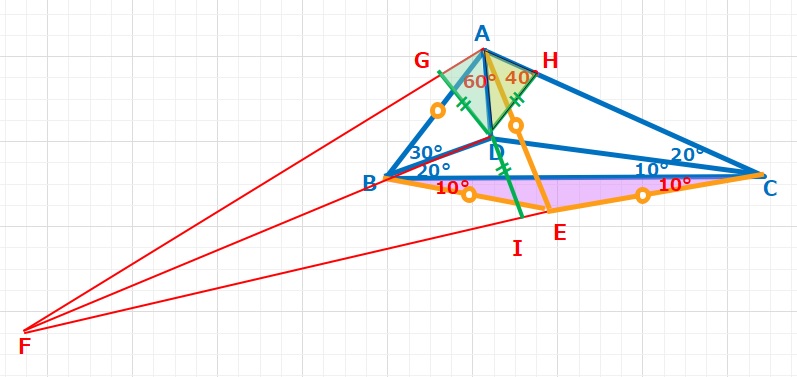
△AFCにおいて ∠ACD=∠FCD=20°、∠EFD=∠AFD=10°より
△CEDと△CHD,△IFDと△GFDはそれぞれ合同な三角形となりますので、
DI=DH=DGとなります。よって △DAGと△DAHも合同となり、∠HAG=40+60+20=120°なのでX=∠BAD=60-20=40° ・・・(答え)
コメント