2021年算数オリンピックトライアル出題問題
【問題】図は正三角形と、2つの正方形と、正六角形を点線で折るとぴったり
重なるようにしたものです。正三角形の1辺のながさが36㎝のとき、
濃い色のついた部分の面積は何㎠ですか。
【ヒント】
水色の図形と赤線の図形は、それぞれ1:2の関係になっています。
これがすべてなのですが、なかなか解答にたどり着きません。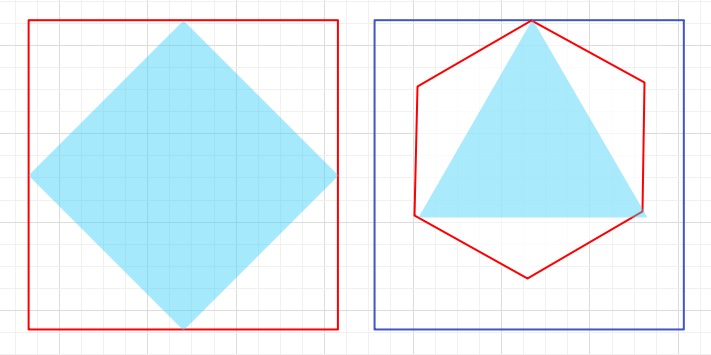
【解答】
(求める面積)=(赤線の正方形)ー(赤線の正六角形)
={(水色の正方形)-(正三角形)}×2
①の三角形は15°の直角三角形なので、2つあわせると
一辺が36㎝、角度が30°の二等辺三角形となり面積は36×18×\(\displaystyle\frac{1}{2}\)=324
②の直角二等辺三角形は36×36×\(\displaystyle\frac{1}{4}\)=324
よって(水色の正方形)-(正三角形)=324+324=648
求める面積は648×2=1296㎠・・・(答え)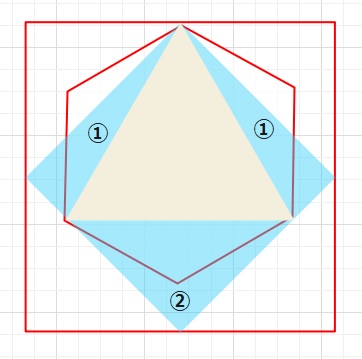
コメント