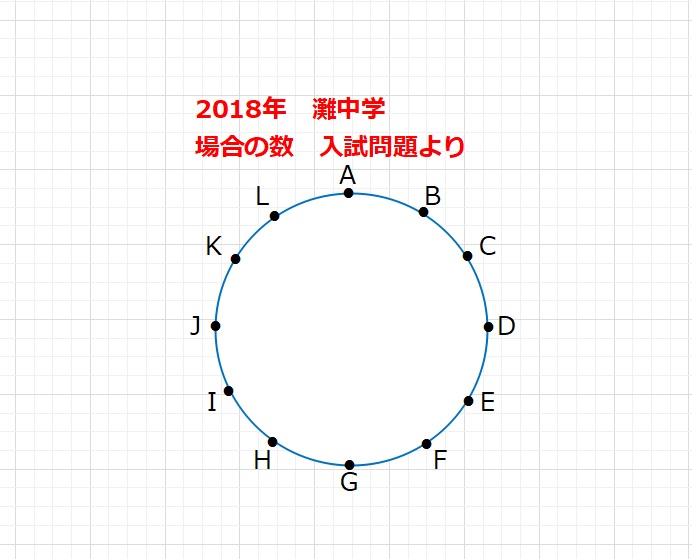
灘中学 2018年入試問題より
【問題】上の図で、円周を12等分した点をA,B,…,Lとします。これら12個の点から異なる3点を選んで三角形をつくるとき、どの辺の長さも円の半径より大きくなるような三角形は全部で ア個あります。ただし、合同な三角形でも、頂点が異なるときには異なる三角形として数えます。
【ヒント】場合の数の問題を解くにあたり重要なことは、与えられたルールを把握して、
下記をヒントにもれなく仕分けすることです。与えられたルールをわかりやすく置き換えることも
重要なカギを握ります。
①もれなくダブりなくカウントする。
②複雑な場合は、小分けにしてグループ別に考えていく
③場合分けのパターンを少しでも減らすために、固定したり、まとめてペアにして減らしたりする
④多いパターンではなく、少ないパターンの方を数える
今回の問題では「どの辺の長さも円の半径より大きくなる」ということを
中心にグループ分けします。
下図のとおり、まず点Aを固定します。1つ飛ばしたKとAを結んだ辺の長さ
は紫の三角形が正三角形ですので、半径と同じ長さになることがわかります。
よって、点と点を結ぶときに少なくとも間に2点以上ないといけないことがわかります。
①AJを1辺とする場合
②AIを1辺とする場合
③AHを1辺とする場合
④AGを1辺とする場合
で仕分けできそうです。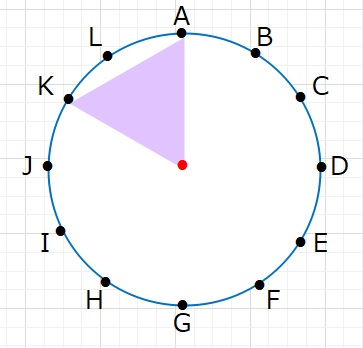
【解答】
①AJを1辺とする場合 4通り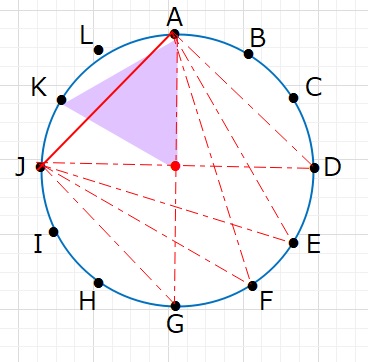
②AIを1辺とする場合 3通り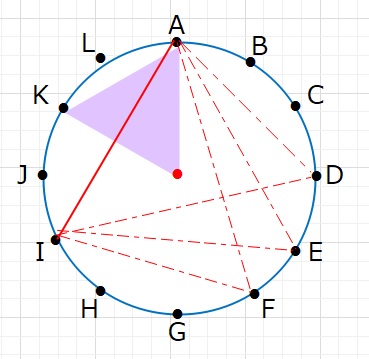
③AHを1辺とする場合 2通り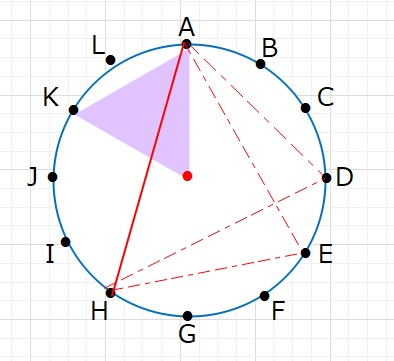
④AGを1辺とする場合 1通り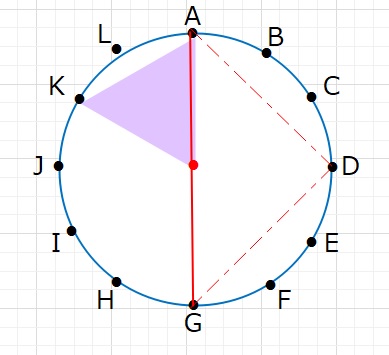
以上より Aを固定した際に、4+3+2+1=10通りの三角形があります。
それぞれの点に対して同じことが言えますので、10×12=120通りとなります。
しかし、3つの点を選ぶため同じ三角形を3回カウントしてますので、
120÷3=40通り・・・(答え)となります。

コメント