★★★☆☆中級コース　あまりの問題

2.5
灘中 2019年入試問題より

【ヒント】あまりのグループ分けの問題は、前回ご紹介した、数の式の武器　modを理解していると簡単に解答できます。
まず、377がどんな数が知るために、素数で分解します。
素数で分解する方法も、以前ご紹介してますのでそちらを参照ください。
これも以前紹介しましたが、１から１００までの素数は25個ありますから、おさえておきましょう。
377＝13×29ですね。 377を5回かけた数は表現が面倒くさいので、これまた以前紹介した累乗を活用して　\(377^{5}\) ＝\((13)^{5}\)×\((29)^{5}\)とかきます。

【解答】
約数の組合せは　\((13)^{0}\)=1に29を０－5回かけた6個　
\((13)^{1}\)に29を0-5回かけた6個・・・
と、6×６＝３６通りあります。　29は何回かけても14で割った余りは１ですので、
組合せとしては　1×１＝１となる　1 ,\((13)^{2}\), \((13)^{4}\), \((13)^{6}\)
の４とおりに対してそれぞれ29を0-6回かけた7とおりとの組み合わせで
7×４の28とおり・・・（答え）となります。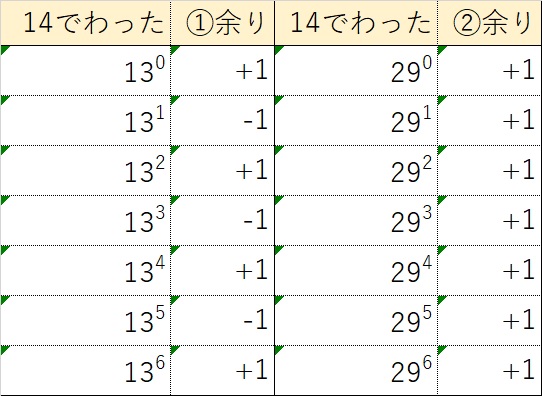

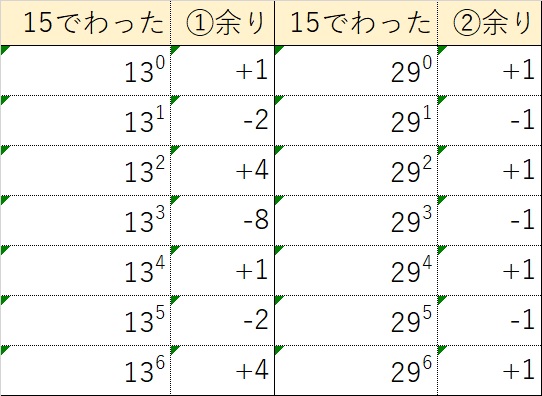
同様に15でわった時を一覧にすると、下の表のようになり、
余りが１になる組合せは、\((13)^{0}\)=1　と29を0回、2回、4回、6回かけた組合せと、
\((13)^{4}\)　と29を0回、2回、4回、6回かけた組合せの
８とおり・・・（答え）となります。
modの考え方を使うと簡単に解答できますね。