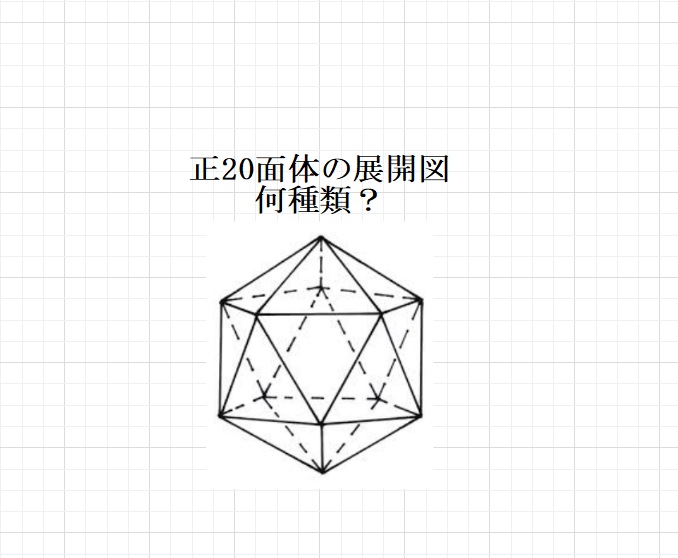
【問題】図のように正五角形が12枚とそのまわりを取り囲むように
正六角形が並んでいるサッカーボールのような物体があります。
(1)正六角形は全部で何個ありますか。
(2)辺の数は全部で何本ですか。
【ヒント】正多面体の頂点、辺の数え方が頭にはいっていれば簡単です。
以前ご紹介したものを参考にしてください。
★★☆☆☆初級コース 正12面体の展開図 | 算数コロシアム (mathcolo.com)
を参考にしてください。
【解答】
(1)正五角形を取り囲んでいるので、1つの正五角形に正六角形は5枚あります。
それが12枚あるので、5×12=60枚あります。
あとは重複をカウントすればよいです。図をみると1つの正六角形を3回カウント
することになるので、60÷3=20枚・・・(答え)
(2)正五角形の辺の数は5本、これが12面あるので12×5=60本の
辺があります。さらに、正五角形の頂点から5本の辺(合計60本)
が出ていますが、この辺は重複しています。
1つの辺を2回カウントしているので、60÷2=30本となります。
よって辺は60+30=90本・・・(答え)
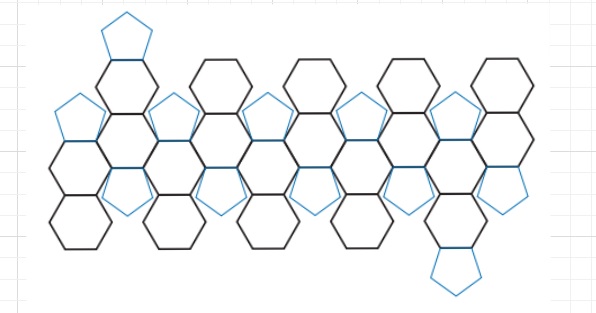
【オマケ】これは切頂20面体といわれる形で、一番シンプルな
展開図(主観ですが)は下のような形になります。
ちなみに、切頂20面体は32面体といわれ、それをしってると、1番の答えは
即答ですね(笑)。

コメント