★★★☆☆中級コース　正三角形の面積

2.5

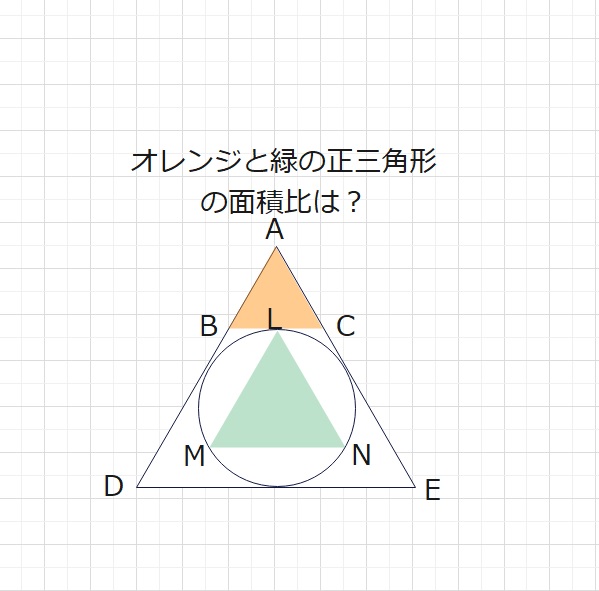
【問題】図のような３つの正三角形と円があるとき、正三角形ABCとLMNの面積比
はいくつですか。

【ヒント】とても難しく感じる人もいるかもですが、
三角形LMNを180°回転すると、下の左の図の緑のようになります。
ということは、左の図のように正三角形で三角形ADEの中を敷き詰めることができます。
また、下の右図のように、オレンジの正三角形も正三角形ADEの中を
敷き詰めることができます。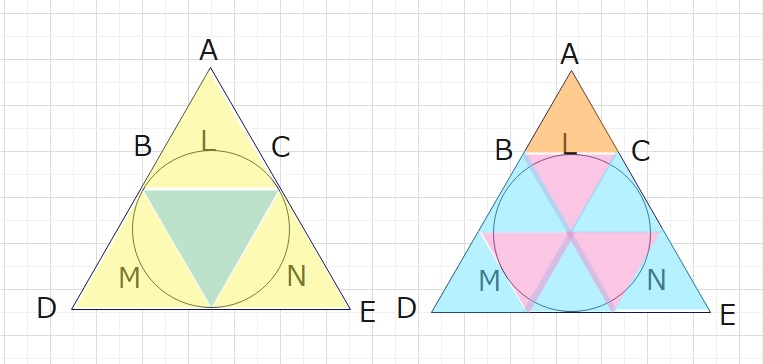

【解答】正三角形ADEは緑の正三角形4個分、オレンジの正三角形9個分とわかります。
今正三角形ADEを１とすると　
△LMN＝\(\displaystyle\frac{1}{4}\),△ABC=\(\displaystyle\frac{1}{9}\)

となり、△LMN:△ABC=\(\displaystyle\frac{1}{4}\)：\(\displaystyle\frac{1}{9}\)

＝９：４・・・（答え）