2022年 神戸女学院中入試問題より
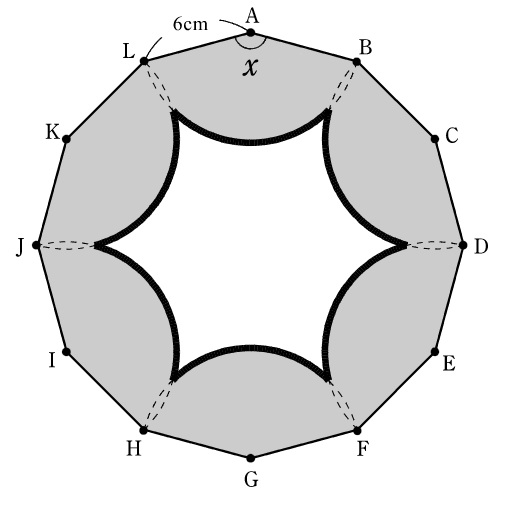
【問題】図のような一辺が6㎝の正12角形ABCDEFGHIJKLがあり、
頂点A,C,E,G,I,Kを中心とする半径6㎝のおうぎ形をかきます。
円周率は3.14とします。
(1)xの角の大きさを求めなさい。
(2)図の太線の長さを求めなさい。
(3)図の色のついた部分の面積を求めなさい。
【ヒント】
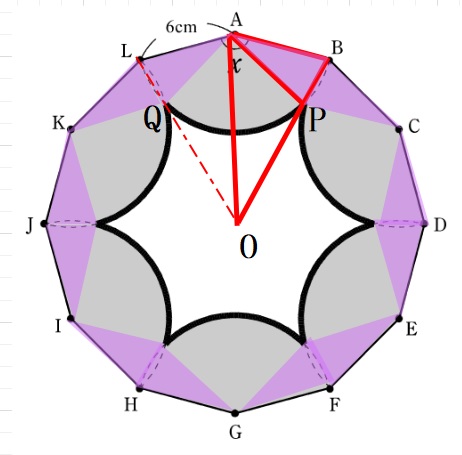
下図のように点O、点Pとすると、△OABと△APBは相似な二等辺三角形となります。
∠AOBは 360°÷12=30 °となります。
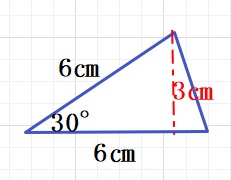
30°の二等辺三角形は図のように30°、60°、90°の直角三角形
をつくり、面積が求めることができます。
【解答】
(1) x=∠OAB×2=∠OAB+∠OBA
∠AOB=30°なので、x=180-30=150°・・・(1)の答え
(2)∠QAP=150-∠LAQ-∠PAB=150-30-30=90°
図の太線は 半径6㎝の半円 6個分の周の長さ、つまり半径6㎝の円周の1.5倍とわかります。
2×6×3.14×\(\displaystyle\frac{3}{2}\)=18×3.14=56.52㎝・・(2)の答え
(3)求める面積は 半径6㎝の半円6個分と頂角30°の二等辺三角形12個の合計となります。
6×6×3.14×\(\displaystyle\frac{3}{2}\)+6×3×\(\displaystyle\frac{1}{2}\)×12
=54×3.14+9×12=54×3.14+54×2=54×(3.14+2)=54×5.14
=277.56㎠・・・(3)の答え
コメント