2019年六甲中学 入試問題
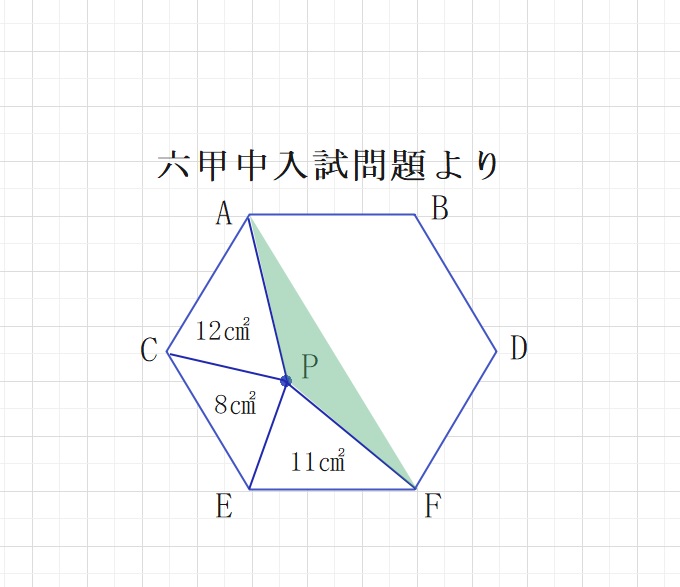
【問題】図のようにABCDEFと点Pがあります。
△PAC、△PCE、△PEFの面積がそれぞれ12㎠、8㎠、11㎠であるとき、
△PAFの面積は何㎠ですか。
【ヒント】
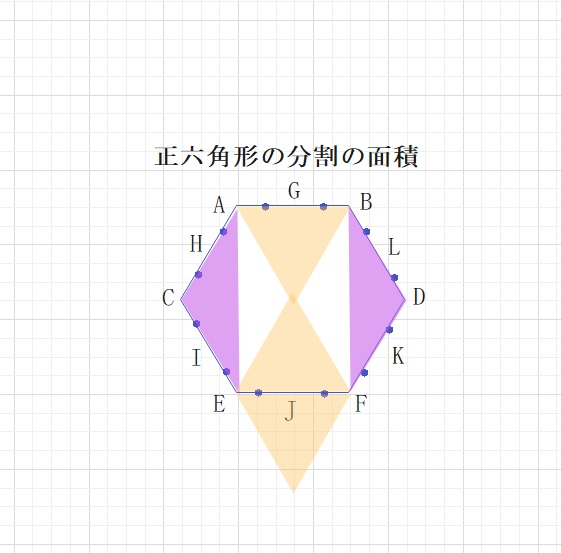
この手の問題を解く場合、以前図形問題の武器 正六角形の面積で紹介した
正三角形QCEを書くことがポイントとなります。
この問題はよくでるパターンなのでしっかり押さえておきたいです。
△PQCと△PAC、△PQEと△PEFは高さと底辺がそれぞれ等しいため
面積が等しくなります。
ゼロから始める図形問題の武器 正六角形の面積 | 算数コロシアム (mathcolo.com)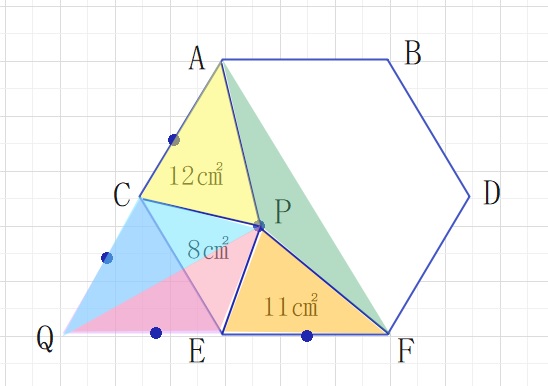
【解答】
△PQC=△PAC=12、△PQE=△PEF=11より
四角形AQFP=12×2+11×2=46となります
よって△QEC=46ー(11+12+8)=15となり
これは正六角形の\(\displaystyle\frac{1}{6}\)です。
よって正六角形の面積は15×6=90となり
四角形CEFA=90÷2=45となります。
求めるPAF=45-(12+11+8)=14㎠・・・(答え)
コメント