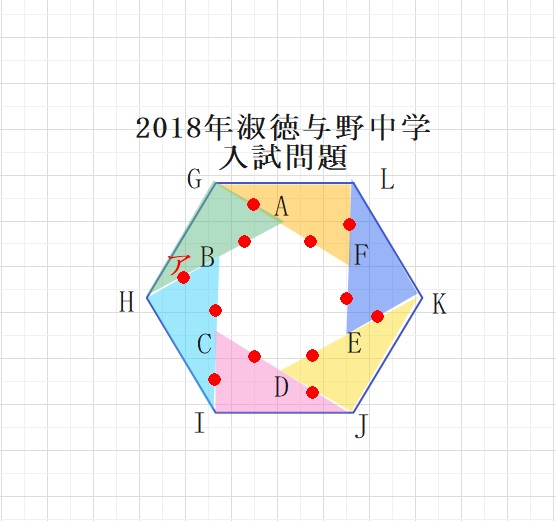
2018年 淑徳与野中学入試問題より
【問題】図のように正六角形ABCDEFとGHIJKLがあります。
点A,B,C,D,E,FはそれぞれFG,AH,BI.CJ,DK,ELの真ん中の点です。
(1)角アは何度ですか。
(2)三角形AGHの面積は三角形ABCの面積の何倍ですか。
(3)正六角形GHIJKLの面積は、正六角形ABCDEFの面積の何倍ですか。
【ヒント】複雑にみえますが、基本的な考え方の組合せです。
長さの等しい直線がたくさんあらわれ、面積の等しい三角形で分割できます。
正六角形の1つの角は120°ですので、∠HAG=180-120=60°となります。
HAの長さは、AGの長さの2倍ですので、、、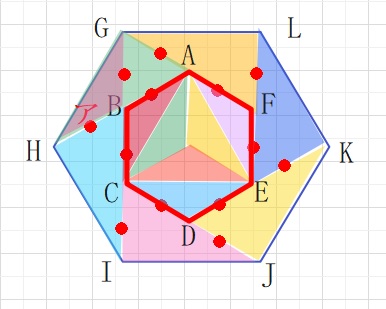
【解答】
(1)三角形HAGにおいて∠HAG=60°、HA:AG=2:1なので
ア=30°・・・(答え)
△HAGは30°、60°、90°の基本の直角三角形とわかります。
(2)△ABCと△GBH,△GBAの面積は等しいので、
△AGHは△ABCの2倍・・・(答え)
(3)正六角形ABCDEFは△ABCの6倍となります。
正六角形GHIJKLは正六角形ABCDEFに△HAGを6個付け加えたもので
これは△ABCを12個付け加えたもの、つまり△ABCの6+12=18倍とわかります。
よって、18÷6=3倍・・・(答え)
コメント