★★★☆☆中級コース　正六角形の分割の面積　早稲田中学入試門題より

2.5
2017年早稲田中学入試問題より

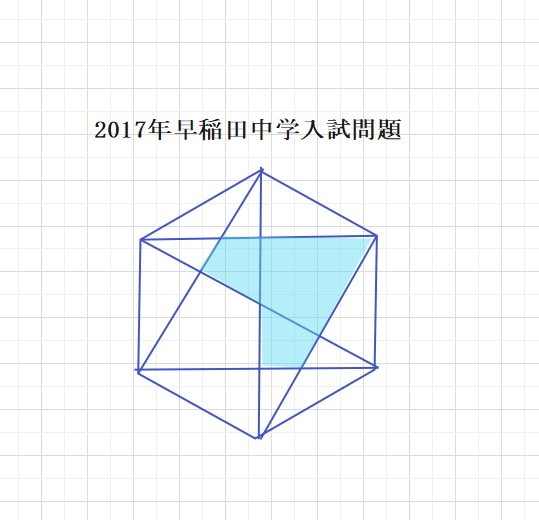
【問題】図の正六角形の面積は６㎠です。色のついた部分の面積は何㎠ですか。

【ヒント】
色々な解き方があると思います。
下図の緑と黄色とオレンジと紫の三角形はすべて正六角形の
\(\displaystyle\frac{1}{6}\)です。

また白の三角形２つ合わせて正六角形の\(\displaystyle\frac{1}{6}\)×\(\displaystyle\frac{1}{3}\)とわかります。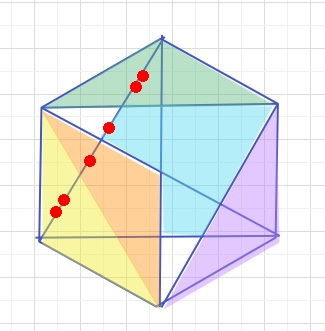

【解答】
正六角形のブルー以外の部分の面積は
正六角形の\(\displaystyle\frac{1}{6}\)の三角形４つと
\(\displaystyle\frac{1}{6}\)×\(\displaystyle\frac{1}{3}\)＝\(\displaystyle\frac{1}{18}\)の三角形１つでできています。
よって\(\displaystyle\frac{1}{6}\)×４＋\(\displaystyle\frac{1}{18}\)＝\(\displaystyle\frac{12+1}{18}\)=\(\displaystyle\frac{13}{18}\)となります。

ブルーの面積は１－\(\displaystyle\frac{13}{18}\)＝\(\displaystyle\frac{5}{18}\)

今正六角形の面積は６なので\(\displaystyle\frac{5}{18}\)×６＝\(\displaystyle\frac{5}{3}\)

求める面積は　１\(\displaystyle\frac{2}{3}\)･･(答え)