2021年 清風南海中入試問題より
【問題】
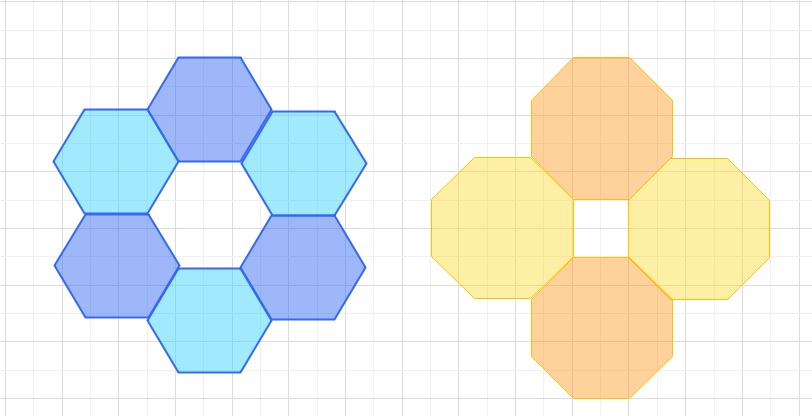
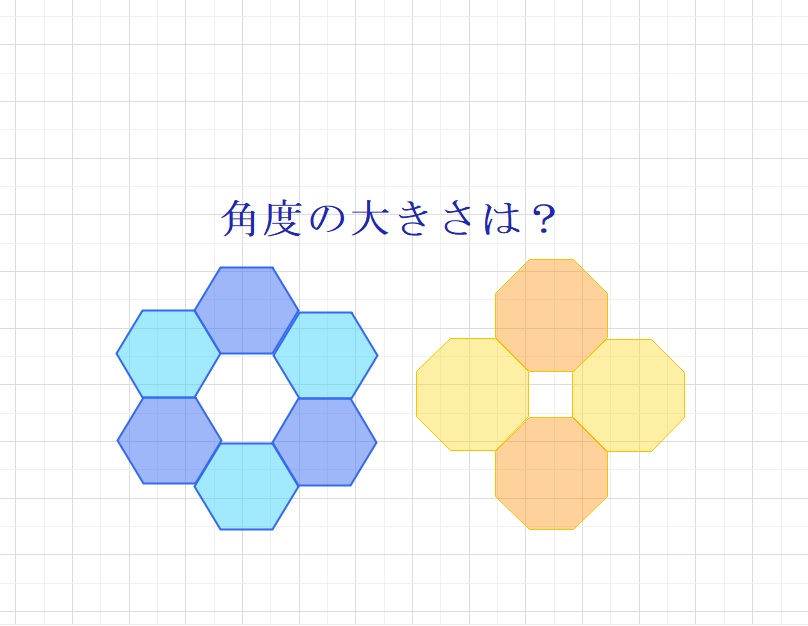
図のように,同じ大きさの正六角形を辺が重なるように6個並べると、
それらに囲まれた部分は正六角形となります。
また、同じ大きさの正八角形を辺が重なるように4個並べると、
それらに囲まれた部分は正方形となります。これと同じよう、
同じ大きさの正五角形を辺が重なるように[ア]個並べると、
それらに囲まれた部分は正[ア]角形となります。
また、同じ大きさの正[イ]角形を辺が重なるように3個並べると、
それらに囲まれた部分は正三角形となります。
[ア][イ]に当てはまる数を答えなさい。
【ヒント】
以前ご紹介した、正多角形の内角の和をご参考下さい。
ゼロからはじめる 図形の武器4 多角形の内角の和 | 算数コロシアム (mathcolo.com)
正5角形の内角の和は、180×3=540°となります。
1つあたりの角度は540÷5=108°です。
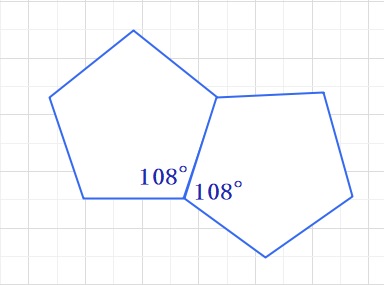
イはアの求め方と同じ考え方で求めることができます。
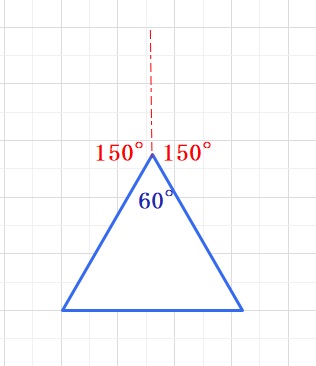
逆に真ん中にできる図形が正三角形とわかってますので、
周りにできる正多角形の1つの内角は150°とわかります。
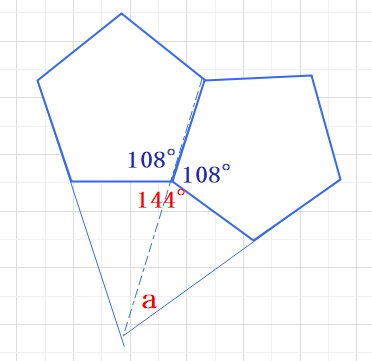
【解答】図の正五角形の内側?の角度は360-108×2=144°となります。
よってaの角度は180-144=36°となり、
360÷36=10なので、正10角形ができることになります。
ア=10・・・(答え)
中心の角は 180-150=30°なので360÷30=12となります。
よって イ=12・・(答え)

コメント