★★★☆☆中級コース　正多面体は何個ある？

結論を先に言いますと、5種類です。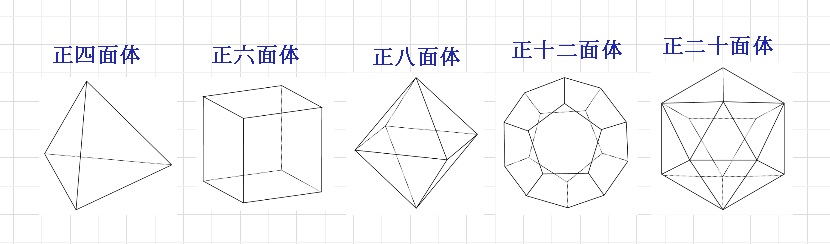


なぜでしょうか？
まず、「正多面体の定義」を見てみます。
正多面体とは、
１．すべての面が合同な正多角形
２．どの頂点に集まる面の数も同じ
３．すべての頂点は同一球面上にある　
をすべて満たす、多面体のことをいいます。３はよくわかりませんが、
へこんでいない（凸型である）と解釈しましょう。

以上を踏まえ、まず
■正三角形によってできる正多面体について考えます。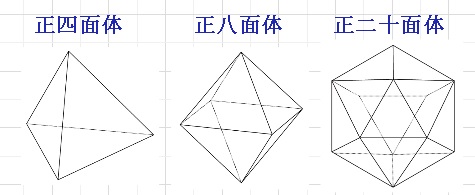

正四面体は、1つの頂点に3つの正三角形が集まっています。
正八面体は、1つの頂点に4つの正三角形が集まっています。
正十二面体は、1つの頂点に5つの正三角形が集まっています。

ここで、1つの頂点に6つの正三角形を集めますと、、、
下のような形になり、平面になってしまいます。
また、1つの頂点に60°×6=360°以上があつまるとへこんだ形となります。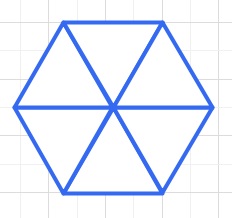

次に、
■正四角形によってできる正多面体について考えます。
これは、下の正六面体（立方体）があります。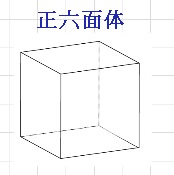

正三角形のときと同様に考えますと、4つの正四角形（正方形）をあつめると
平面になり、1つの頂点に90°×4=360°以上があつまるとへこんだ形となります。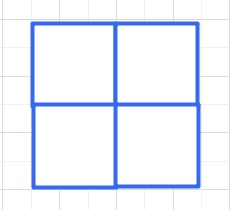


次に
■正五角形によってできる正多面体です。
これは正十二面体となり、正五角形が3個集まってできています。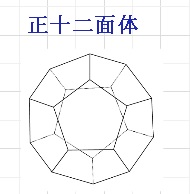

同様に考えると、正五角形の1つの角は108°ですので、108×4＝432°となり、
360°を超え、形がへこんでしまいます。

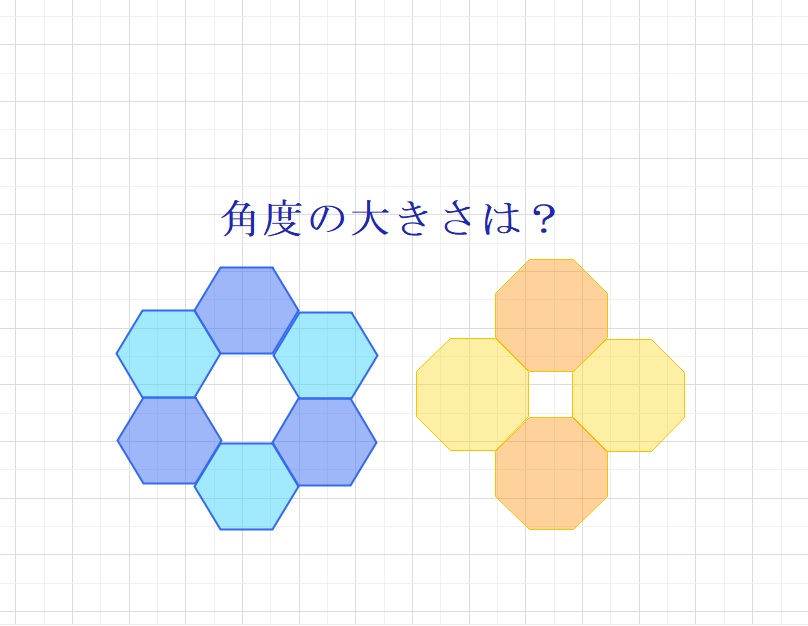
■正六角形の1つ角は120°ですから、360÷120＝３となり、
3つの正六角形を集めると平面になってしまいます。
2つの正六角形では立体はつくれませんので、これ以上の正多角形をつかって
正多面体を作ることは無理ということがわかります。

以上より、正多面体は5種類しかありません。　（証明終了）