2018年 灘中学入試問題より
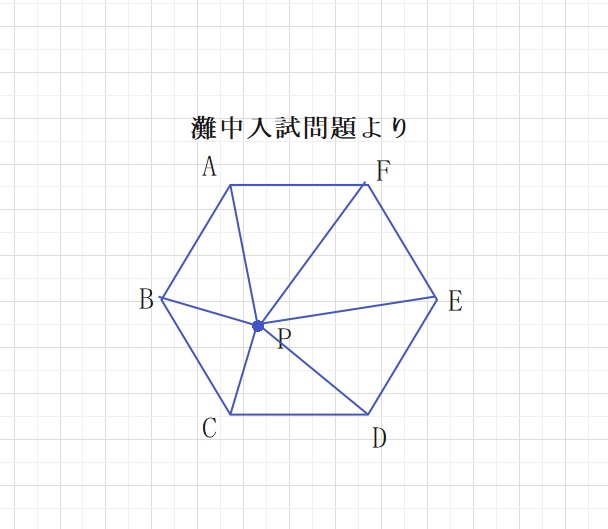
【問題】図のように正六角形ABCDEFの内側に点Pをとり、
6つの頂点とPをそれぞれ直線で結びます。三角形ABP,CDP,EFP
の面積がそれぞれ、3㎠,5㎠,8㎠であるとき、
三角形BCPの面積はア㎠です。
【ヒント】何度かご紹介してきたものと一緒です。この手の問題は、
解き方がほぼ決まっています。
詳しくは以前ご紹介した、「図形の武器」正六角形の面積をみてください。
ゼロから始める図形問題の武器 正六角形の面積 | 算数コロシアム (mathcolo.com)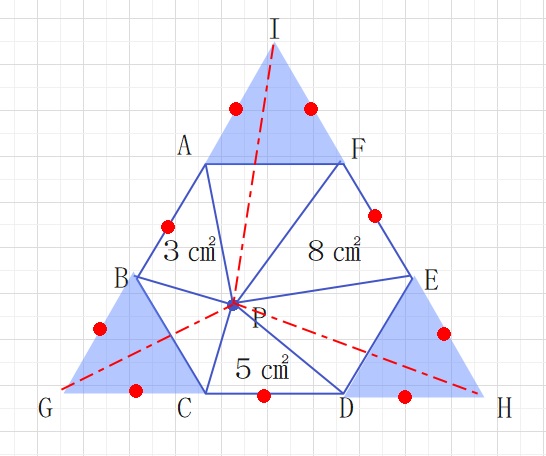
【解答】正六角形の2つの辺を延長してできた正三角形IAF,GBC,HDEを作ります。
この3つの正三角形はもとの正六角形の面積の\(\displaystyle\frac{1}{6}\)です。
また三角形PIAとPAB、PBGは底辺と高さが等しいのでともに3㎠となります。
同様に三角形PGC、PCD、PDHはともに5㎠となり、
三角形PHE、PFE、PIFはともに8㎠となります。
よって大きな三角形IGHの面積は3×3+5×3+8×3=48㎠となります。
この正三角形は小さな正三角形(IAFなど)9個分となりますので、
小さな正三角形1つの面積は\(\displaystyle\frac{16}{3}\)となります。
よって三角形BCPの面積は
四角形GCPBー三角形BGC=3+5-\(\displaystyle\frac{16}{3}\)=\(\displaystyle\frac{8}{3}\)
よってアの面積は2\(\displaystyle\frac{2}{3}\)㎠・・(答え)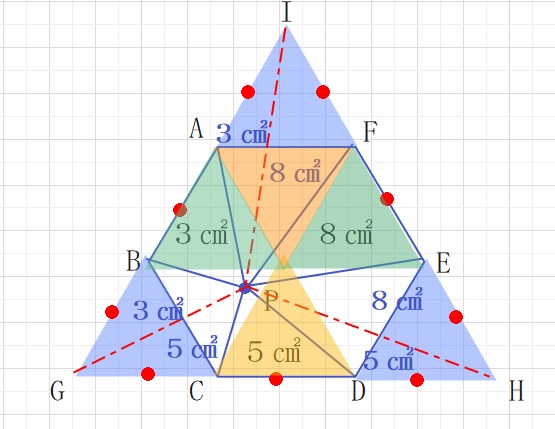
コメント