今回は食塩水の問題で前回紹介した、面積の図やてんびん図が使いにくい問題を
ご紹介します。基本に戻って考えてみましょう。
食塩の問題を解く際に重要なのは、(食塩の量)g=(濃度)%×(食塩水の量)gで、
食塩の量に注目して、解くことが重要です。
【例題1】16%の食塩水400gから
食塩水100gを取り出して、水を100g入れてよくかき混ぜ、
また食塩水200gを取り出して、水を200gを入れてよくかき混ぜました。
できた食塩水の濃度は何%ですか。
【解答】
16% 食塩水400gには16×\(\displaystyle\frac{1}{100}\)×400=64gの食塩が入っている
100gには16g入っているので 64-16=48gの食塩になった
400gで48gなので\(\displaystyle\frac{48}{400}\)×100=12%
さらに200g(この中には食塩24g)を抜くと48-24=24gの食塩が入っている。
よって\(\displaystyle\frac{24}{400}\)×100=6%・・・(答え)
これまでを図で書くと下図のようになります。
【例題2】2つの食塩水A、Bがあります。Aの食塩水300gとBの食塩水300gを混ぜると11%
の食塩水になり、Aの食塩水60gとBの食塩水20gを混ぜると14.5%の食塩水に
なります。Aは何%の食塩水ですか。
【解答】
①A 食塩水300g B 食塩水 300g=11%食塩水600g→食塩の量66g
②A 食塩水60g B 食塩水 20g=14.5%食塩水80g→食塩の量11.6g
②×5より ③A食塩水 300g B食塩水 100g=14.5%食塩水400g→食塩の量 58g
①-③より B食塩水200g =200g食塩水 8g
となり、 Bの食塩水は \(\displaystyle\frac{8}{200}\)×100=4%
③より A食塩水 300gには 食塩が58-4=54g 含まれることとなる。
よって A 食塩水は \(\displaystyle\frac{54}{300}\)×100=18% ・・・(答え)
【例題3】2つの食塩水A、Bがあります。濃さの比は8:5で、
Aの食塩水300gとBの食塩水150gを混ぜると濃さは14%になります。
Aは何%の食塩水ですか。
【解答】
A:B=8:5 なので、5×A=8×B A=\(\displaystyle\frac{8}{5}\)×B
③=\(\displaystyle\frac{8}{5}\)×BーB=\(\displaystyle\frac{3}{5}\)×B
①=\(\displaystyle\frac{1}{5}\)×B
B+\(\displaystyle\frac{2}{5}\)×B=\(\displaystyle\frac{7}{5}\)×B=14
B=14×\(\displaystyle\frac{5}{7}\)=10%
よって,A=\(\displaystyle\frac{8}{5}\)×10=16%・・・(答え)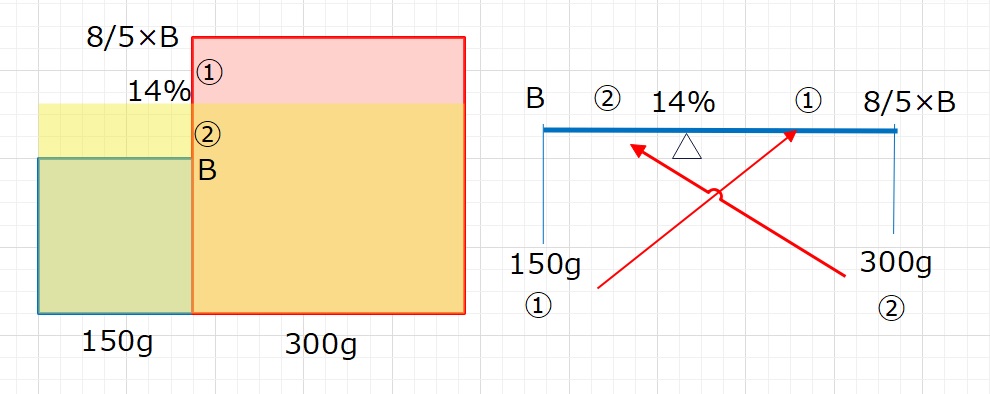
コメント