灘中 2022年入試問題より
【問題】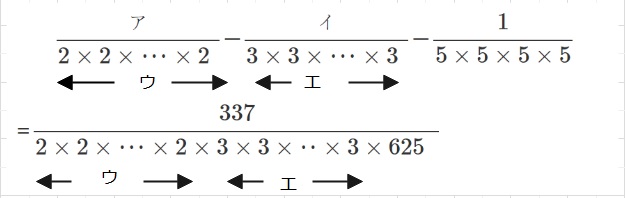
のアに整数を、イに1以上9以下の整数を、ウ、エに2以上5以下の整数をあてはめて、
この式を完成しました。この時アに当てはまる整数はなんですか。
【ヒント】ウは 4,8,16,32 エは 9,81,729,6561のいずれかとなります。
式の表現が複雑なので、累乗の表現を使用させてもらいます。
\(\displaystyle\frac{ア}{2^{ウ}}\)ー\(\displaystyle\frac{イ}{3^{エ}}\)=\(\displaystyle\frac{337}{2^{ウ}×3^{エ}×625}\)+\(\displaystyle\frac{1}{625}\)=\(\displaystyle\frac{337+2^{ウ}×3^{エ}}{2^{ウ}×3^{エ}×625}\)
最左辺と最右辺を分母に注目してくらべると、337+\(2^{ウ}\)×\(3^{エ}\) は625の倍数であることがわかります。
【解答】337+\(2^{ウ}\)×\(3^{エ}\) は625の倍数ですので、地道に当てはめていきます。
組合せは (4,9) (4,81)(4,729)(4,6561)(8,9)(8,81)(8,729)(8,6561)
(16,9)(16,81)(16,729)(16,6561)(32,9)(32,81)(32,729)(32,6561) の16通りとなります。
ここで1つ1つ計算するのもよいですが、625は5の倍数ですので、
同様に 337+\(2^{ウ}\)×\(3^{エ}\)も5で割れることになります。
337は5で割ると2余るので全体が5で割り切れるためには、\(2^{ウ}\)×\(3^{エ}\)は
5で割って2不足することになります。
その組み合わせは (-1)×2 2×(ー1) の組合せしかありません。
\(2^{ウ}\)が5で割って(-1)か2になるには (4,9) (4,81)(4,729)(4,6561)
(32,9)(32,81)(32,729)(32,6561)の組合せ
さらに\(3^{エ}\)を5で割ると (4,*)のときはあまりが2
(32,*)のときは余りが 1不足(-1)となります。
個の組合せは、(32,9) (32,729)の2組に絞ることができます。
ちなみに地道に計算すると、下のとおりです。
337+36=373 337+324=661 337+2916=3253 337+26244=26581
337+72=409 337+648=985 337+5832=6169 337+52488=52825
337+144=481 337+1296=1633 337+11664=12001 337+6577=6914
337+288=625 337+2592=2929 337+23328 =23665 337+209952=210289
(32,9)の場合で考えると、
\(2^{ウ}\)=32 ウ=5
\(3^{エ}\)=9 エ=2 となります。
\(\displaystyle\frac{ア}{32}\)ー\(\displaystyle\frac{イ}{9}\)=\(\displaystyle\frac{ア×9ーイ×32}{9×32}\) よってア×9-イ×32=1となるように イに1から9をあてはめていくと、
イ=7のとき、 ア=25で 235-234=1で成り立ちます。
よって ア=25・・・(答え)となります。
根気よく、かつ効率的に当てはめていく必要があります。
もう少しだけ、工夫できそうな気がします。

コメント