難易度
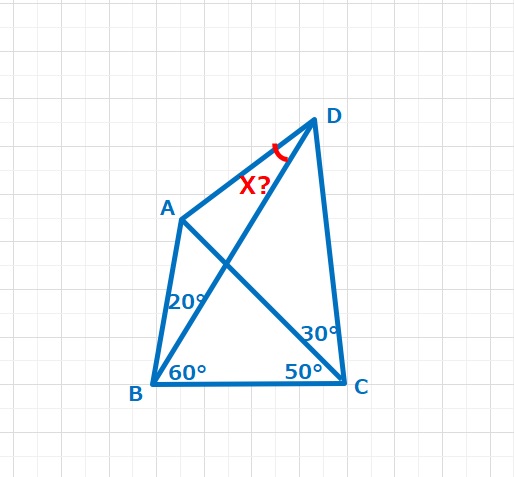
L(20,60,50,30)
本日は以前取り扱った、ラングレー最初の問題の別の解法について考えてみます。気になる方は前回の「ラングレーの最初の問題」をご参照いただいた後で、こちらをご覧いただければと思います。
【解法2】たこ型(kite:凧型)を使った解法。
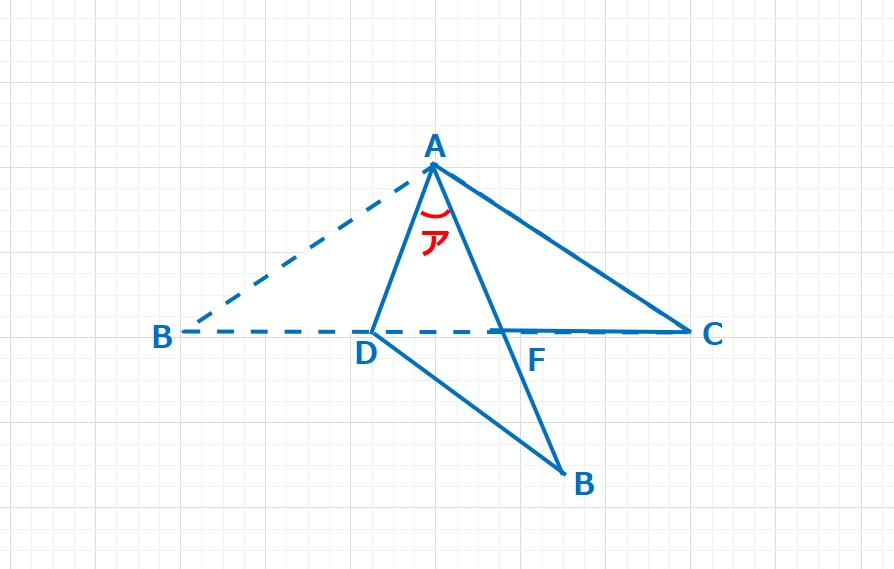
点Dを通り、BCに平行な線EDを引きます。点EはABの延長線との交点です。補助線ECを引くと、線対称な図形が現れます。△FEDと△FBCは、すべての角度が60°なため、正三角形となります。また、∠BAC=50°=∠BCAなので、△BCAは二等辺三角形で、BA=BCです。
BA=BC=BFなので△BAFも二等辺三角形となります。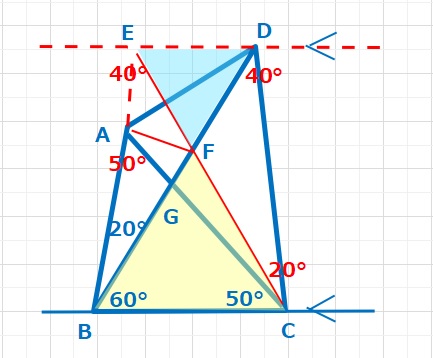
∠BEC=40°、∠EFA=180-∠AFB-∠BFC=180-80-60=40°なので、△AFEは二等辺三角形となり、AF=AEとなります。DE=DFなので、四角形AEDFはたこ型四角形となります。
X=∠ADF=\(\displaystyle\frac{180-80-40}{2}\)=30°・・・(答え)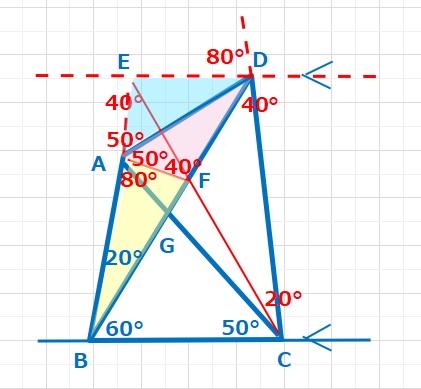
【解法3】扇型(fan型)を使った解法
ABを1辺とした正三角形AEBを書きます。△BEC(ピンク)は20°を頂角とした二等辺三角形となるので、BC=BE。△EDB(ブルー)は∠DEB=100°を頂角とした二等辺三角形となるので、ED=EB。よって図のようにBE=AE=DEとなり、△EDAも頂角40°の二等辺三角形となるので、X=∠ADE-∠BDE=70-40=30°・・・(答え)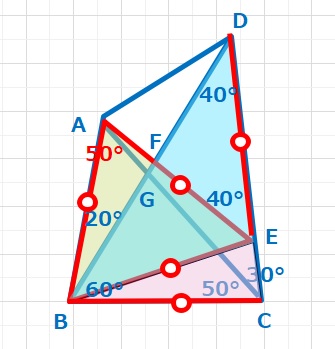
おまけ これは算数の範囲外かもしれませんが、B,A,Dは点Eを中心とした円周上の点となります。∠AEB=60°なので、円周角の定理を使うと、∠ADB=\(\displaystyle\frac{60}{2}\)=30°とすぐにわかります。
他にも解法はありますが、算数の範囲で、他の問題を解く際に武器になりそうなものは前回のものと含めてこの3パターンかと思います。前回触れたとおり、この問題で一番重要なことは、この図形が正18角形の一部であること。正18角形は\(\displaystyle\frac{360}{18}\)=20°を頂角とした二等辺三角形を18個組み合わせた図形です。算数の角度の難問では、よくこの20°の二等辺三角形を題材とした問題が出題されます。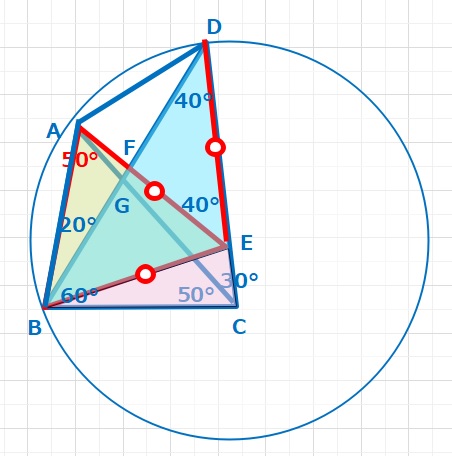
コメント