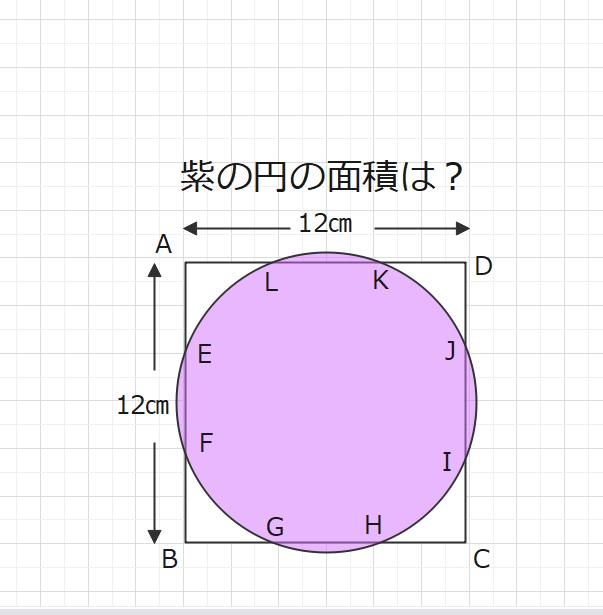
【問題】図のような1辺が12㎝の正方形ABCDで、正方形の辺を3等分する点をE,F,G,H,I,J,K,L
とします。これらの8点をすべて通る円の面積は何㎠ですか。
ただし、円周率は3.14とします。
【ヒント】
気づけば簡単にとけます。
ALの長さは12÷3=4㎝となります。またE,F,G,H,I,J,K,Lはすべて
正方形の1辺を3等分した点なので、その間隔は4㎝となります。
直角三角形KAE=4×8×\(\displaystyle\frac{1}{2}\)=16㎠
正方形EGIKの面積は 正方形ABCD=12×12=144㎠から三角形KAEの4倍を
ひいたものとなります。
また正方形EGIKの面積は 一辺×一辺=EG×EGと表現できますが、
別で表現すると、対角線×対角線×\(\displaystyle\frac{1}{2}\)とも表現できます。
紫の円の面積は 3.14×半径×半径=3.14×OK×OK=3.14×GK×\(\displaystyle\frac{1}{2}\)×GK×\(\displaystyle\frac{1}{2}\)となります。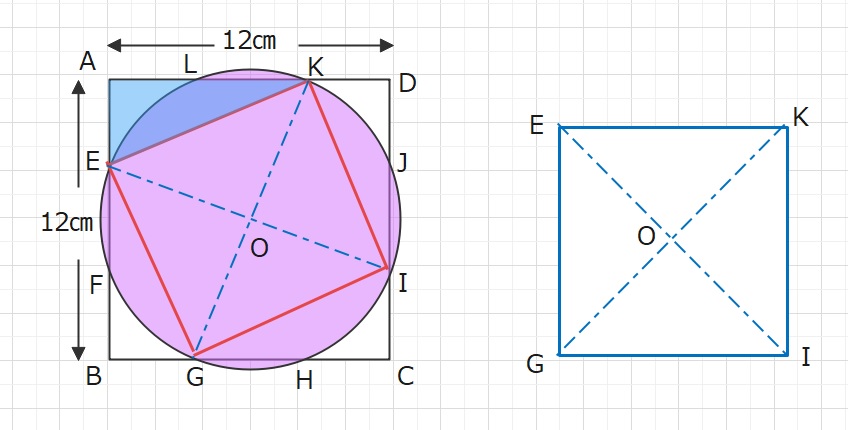
【解答】
正方形EGIK=12×12-16×4=144-64=80=GK×GK×\(\displaystyle\frac{1}{2}\)
紫の円の面積=3.14×GK×GK×\(\displaystyle\frac{1}{2}\)×\(\displaystyle\frac{1}{2}\)
=3.14×80×\(\displaystyle\frac{1}{2}\)=3.14×40
=125.6㎠・・・(答え)
コメント