2019年 灘中入試問題
【問題】
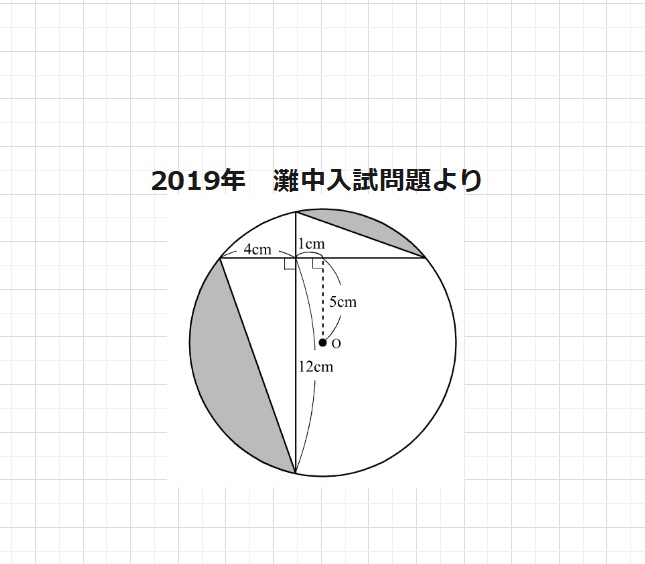
図のような点Oを中心とする円について、色のついた部分の面積の和はあ㎠です。
円周率は3.14とします。
【ヒント】
アの図の面積はイの図へ移動することができます。
よって求める面積あは、半円からブルーの直角三角形の面積を引いたものです。
半円の面積は円の半径がわかれば求まりますが、直接半径を求めるのは難しそうです。
ブルーの面積は緑の四角形より周りの直角三角形3つの面積を引けば求まります。
下の図の右のような正方形を考えると、正方形OABCの面積は10×10÷2=50㎠
正方形OABCの面積は OA×OBと表現できるので
OA×OB=半径×半径=50となります。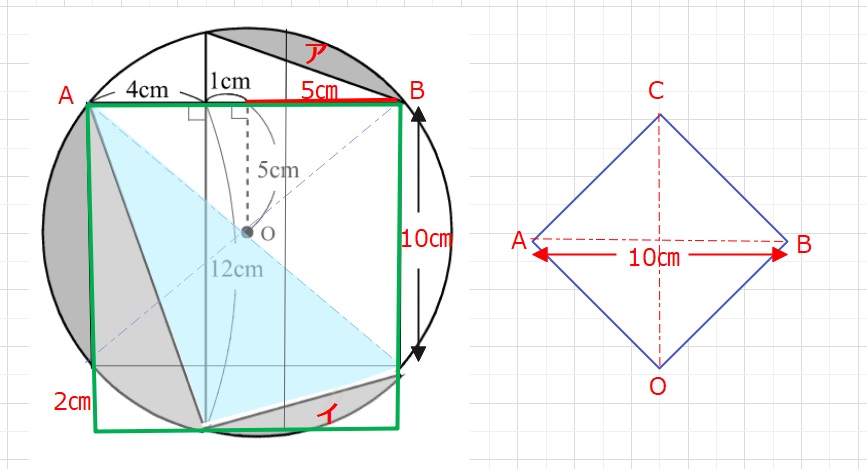
【解答】
半円の面積は OA×OA×3.14×\displaystyle\frac{1}{2}=50×3.14×\displaystyle\frac{1}{2}
=314×\displaystyle\frac{1}{4}=78.5 ㎠
ブルーの直角の面積=12×10-(12×4×\displaystyle\frac{1}{2}+50+6×2×\displaystyle\frac{1}{2})
=120-(24+50+6)=40
よって求める面積は78.5-40=38.5㎠・・(答え)
コメント