★★★☆☆難関コース　四角形の面積　2023年灘中入試問題🔟より

3.0
2023年　灘中入試問題より

【問題】
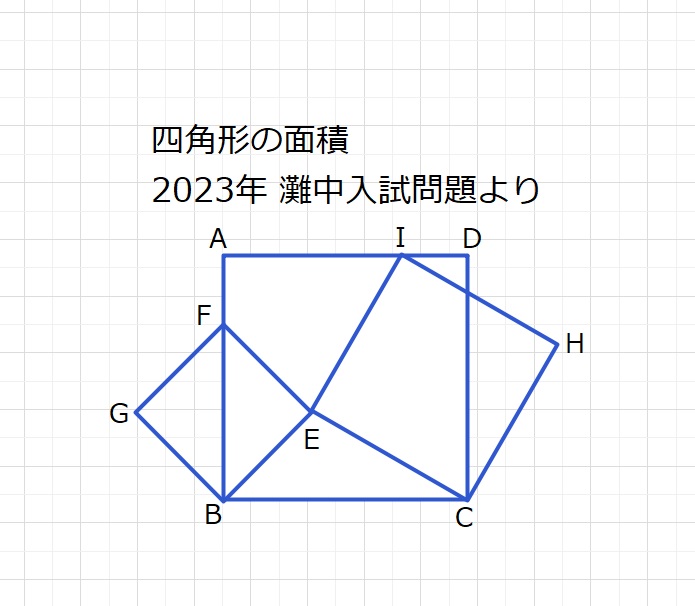
　図の四角形ABCD，BEFG，CHIEはすべて正方形です。
　また、Fは辺AB上に、Iは辺AD上にあります。正方形CHIEの面積が65㎠、
　四角形AFEIの面積と三角形BCEの面積の和が56㎠のとき、
　正方形BEFGの面積はア㎠です。

　【ヒント】ピタゴラスの定理を証明するときに使う、直角三角形と四角形の組合せです。
　　パズル的な思考力が必要です。
　　四角形AFEIと三角形BCEの和が56ですので、△EBKを△FTEに移動すると
　　△EKCと四角形ATEIの和も56㎠となります。
　　

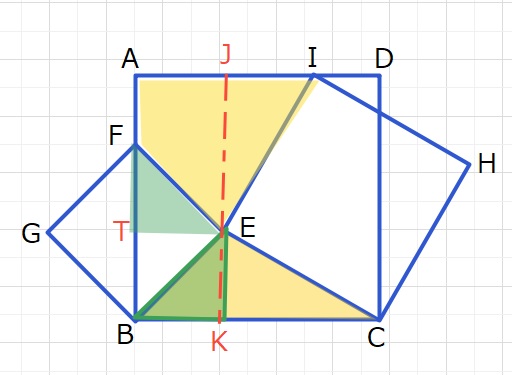
　　さらに四角形ATEJを分割して、△HCLと△IHMに移動します。
　　△JEI＋△EKC+△CLH+△IHM=56㎠となります。
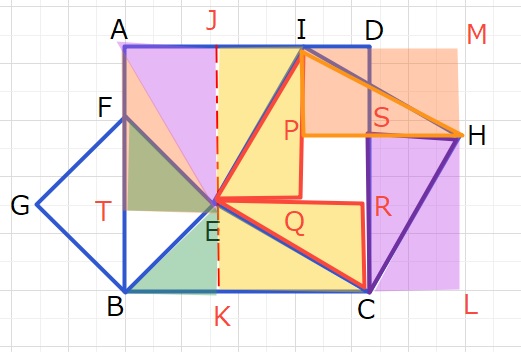
　　四角形IECH=65㎠なので、四角形JKLM＝56＋65＝121㎠
　　四角形PQRS＝四角形IECH-(△JEI＋△EKC+△CLH+△IHM)=65-56=9㎠
　　となります。
　　

【解答】
　四角形JKLM=121㎠なので　11×11＝121よりJK,KL,LM,JMはそれぞれ11㎝
　またPQRS=9㎠なので3×３＝９よりPQ,QR,RS,PSはそれぞれ3㎝となります。
　よってCL＝BK＝EK=(11-3)×\(\displaystyle\frac{1}{2}\)＝4㎝
　もとめる正方形BEFGは△EBK×４＝4×4×\(\displaystyle\frac{1}{2}\)×４＝32㎠
　ア＝32㎠・・・（答え）

【おまけ】
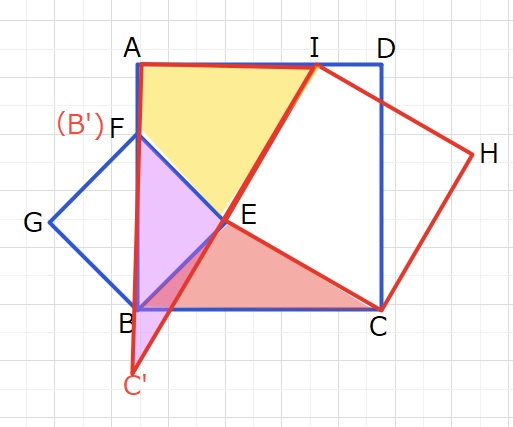
　∠FEB+∠IEC=180°なので　∠FEI+∠BECも180°になるというのがポイントです。
　△EBCを点Eを中心に、90°回転すると、点Bが点Fの位置に行き、IEC’は180°つまり
　一直線になります。よって、△C’AI＋四角形AFEI=△EBC+四角形AFEI
=56+65=121㎠となります。
　

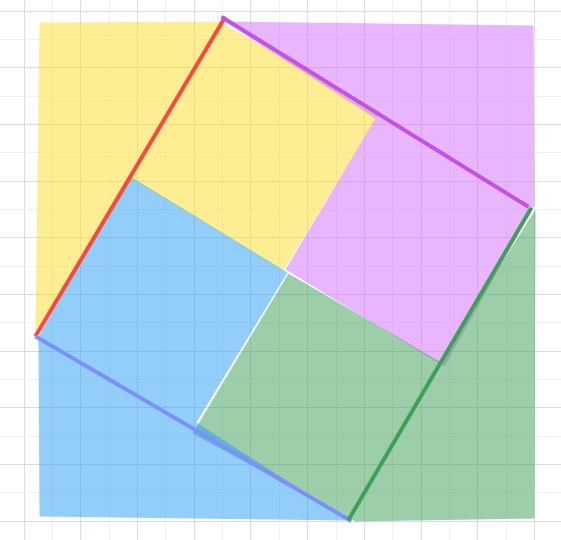
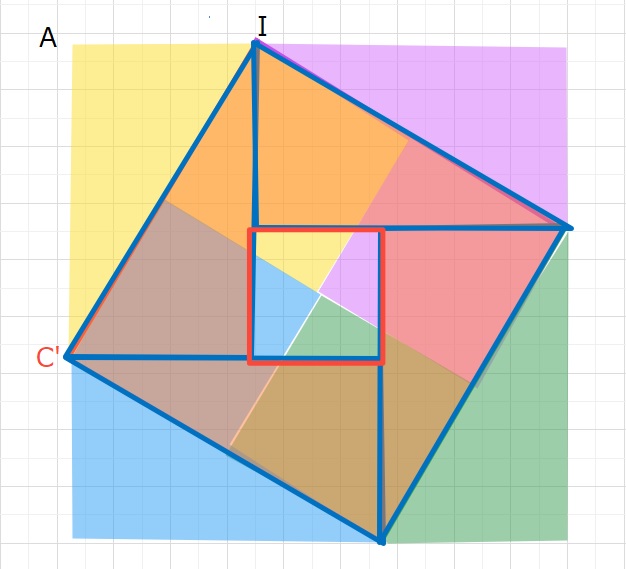
　△C’AI＋四角形AFEIの図形を４つ組み合わせると下のような図形となり、
　面積は121×４＝11×11×2×2=22×22㎠となります。
よって、一辺が24㎝の正方形とわかります。
　

また上の図形に　三角形C’AIを8個敷き詰めると下の図のようになります。
　大きな正方形の面積は22×22＝484㎠なので
　真ん中の赤い正方形は　484－56×８＝484－448＝36㎠となり。
　1辺が6㎝の正方形とわかります。
　AI=（22－6）÷２＝８㎝　これはGE(四角形FGBEの対角線の長さ）と等しいので
　８×８×\(\displaystyle\frac{1}{2}\)=32㎠･･･(答え)