2016年 灘中学入試問題より
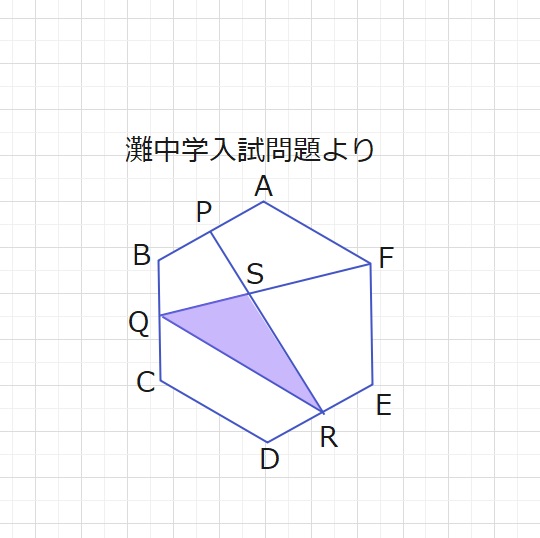
【問題】正六角形ABCDEFがあり、辺AB,BC,DEの真ん中の点を点P,Q,Rとします。
2本の直線PR,QFは点Sで交わっています。
このとき、△QRSの面積は、正六角形ABCDEFのア倍です。
【ヒント】
正六角形ABCDEFの1辺を2とすると、
△MCDと△MQRに注目して MD:MR=2:3=CD:QRとなります
また△SFLと△SQRに注目して LF:RQ=4:3=SF:QSとなります。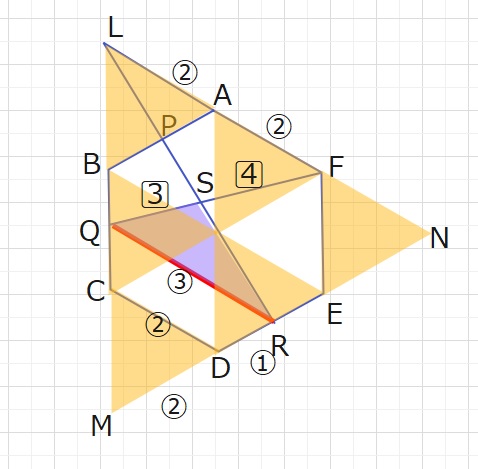
紫の△FQRの面積は、赤の△TQRの面積と等しく、正六角形ABCDEFを
図のように24個の正三角形に分割すると、△TQRは正三角形9個分となるので、
正六角形ABCDEFの\(\displaystyle\frac{9}{24}\)=\(\displaystyle\frac{3}{8}\)倍です。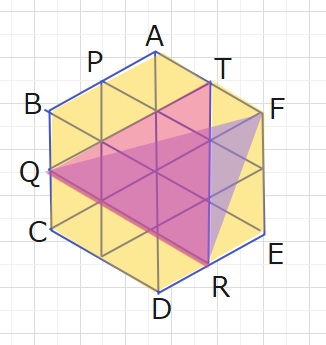
【解答】△FQRは△TQRの面積と等しく、これは正六角形ABCDEFの
\(\displaystyle\frac{3}{8}\)倍となります。
また、△SQRは△TQRの\(\displaystyle\frac{3}{7}\)倍なので、
\(\displaystyle\frac{3}{8}\)×\(\displaystyle\frac{3}{7}\)=\(\displaystyle\frac{9}{56}\)倍・・・(答え)
コメント