2007年 京都女子中学入試問題より
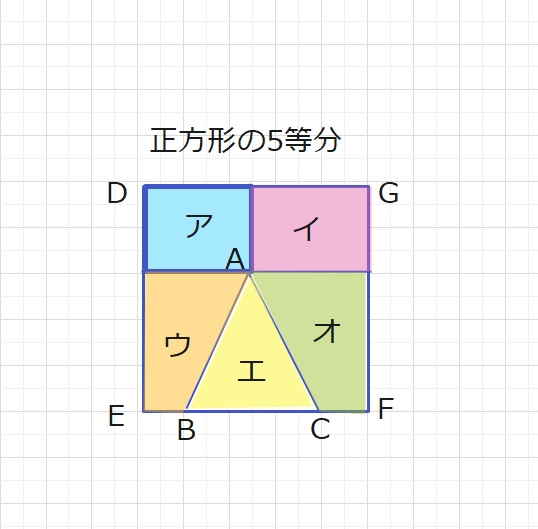
【問題】図のア,イ,ウ,エ,オの図形は、正方形DEFGの面積を5等分したものです。
アとイの図形は長方形、ウとオの図形は台形、エの図形はAB=ACの二等辺三角形で、
アの図形の周りの長さが45㎝のときBCの長さはを求めなさい。
【ヒント】
ア~オの面積はすべて等しいので、DCに注目すると、アとイで分割され、
縦の長さは等しいのでDH=HGということがわかります。
また、次にDEに注目すると、DIにはアとイの2つの図形、
IEにはウとエとオの3つの図形が同じ横の長さ(DG)に入っているので、
DI:IE=2:3となります。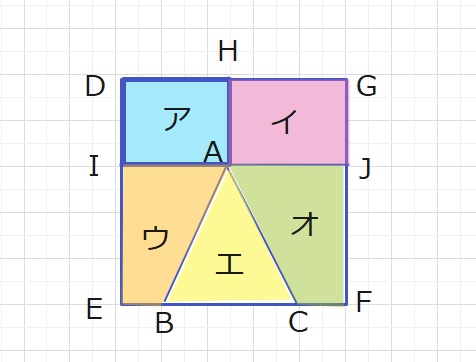
DGとDEの長さは等しいので、比率をそろえると
DH:HG=5:5
DI:IE=4:6 と表現できます。
DIAHの周りの長さ (18)が45㎝に相当するので、
(1)は\(\displaystyle\frac{45}{18}\)=\(\displaystyle\frac{5}{2}\)となります。
あと一ひきですね。5等分の1つあたりの面積は\(\displaystyle\frac{5}{2}\)×5×\(\displaystyle\frac{5}{2}\)×4
=5×5×5=125となり、IE=\(\displaystyle\frac{5}{2}\)×6=15です。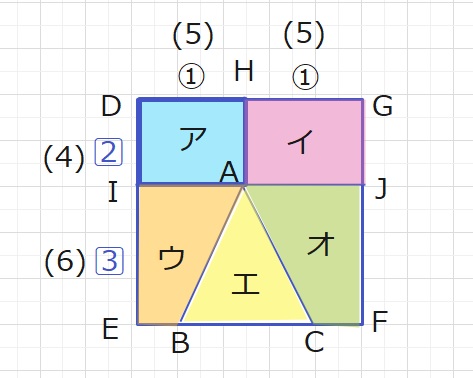
【解答】二等辺三角形 エに注目すると、エの面積は125、高さは15となります。
よって 15×BC×\(\displaystyle\frac{1}{2}\)=125
BC= 125×2×\(\displaystyle\frac{1}{15}\)=\(\displaystyle\frac{50}{3}\)
=16\(\displaystyle\frac{2}{3}\)・・・(答え)
コメント