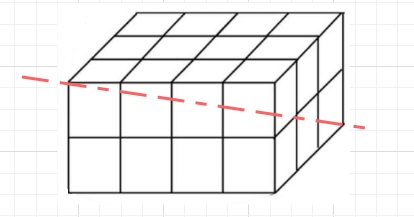
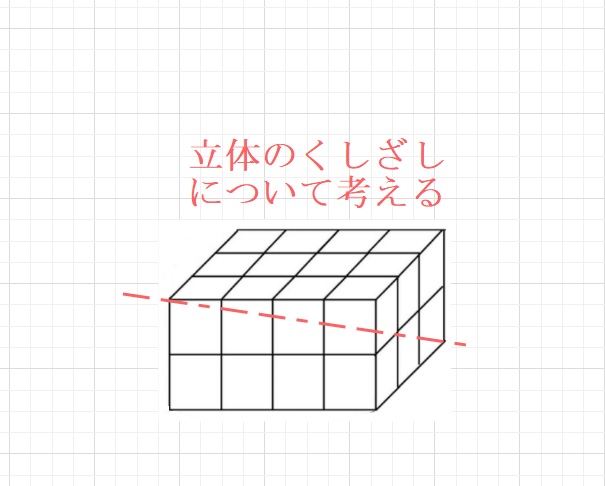
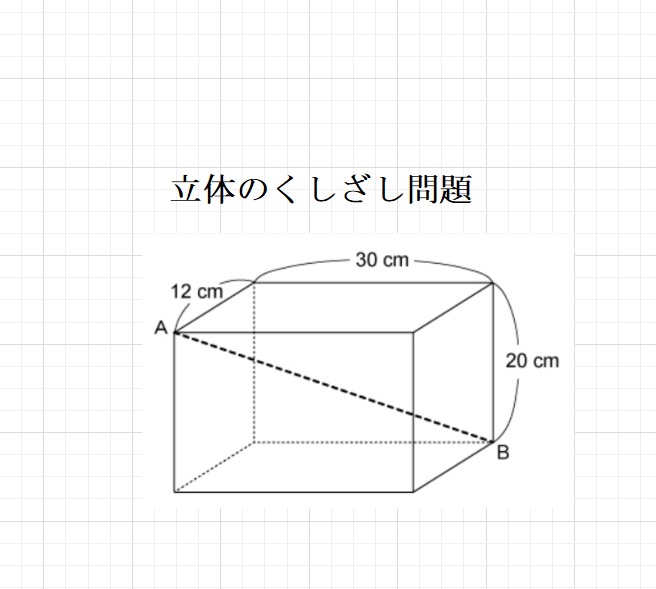
【問題】下図のように、立方体を積んで直方体の頂点から頂点までをまっすぐ
にくしをさしたとき、くしに刺される立法体の個数は全部で何個ですか。
【ヒント】
下図のように3枚の壁を突き抜けるとき、4つの空間をくしざしにします。
つまり、何枚の壁を通過するかを計算すれば、通過する空間の数は求まります。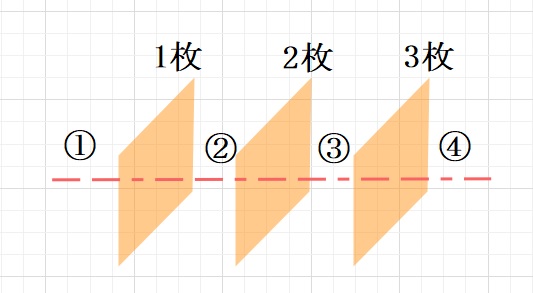
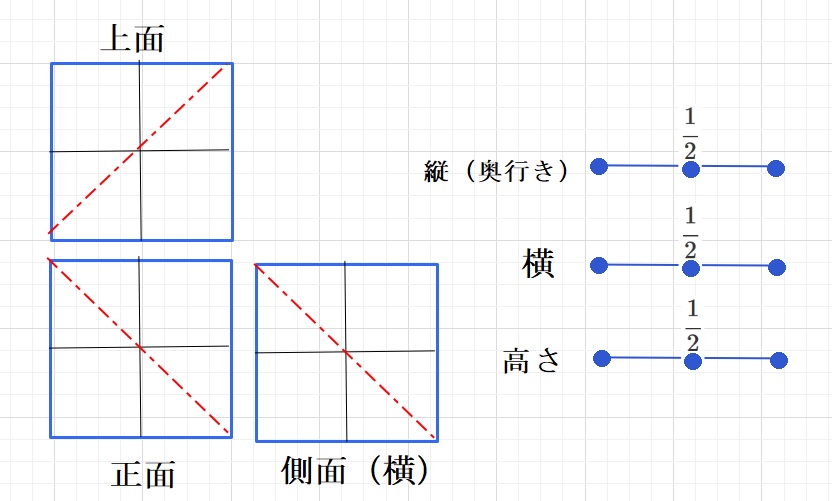
次に、下図のような 横に3個、たて(奥)に2個、高さが1個の
立体を赤線でくしざしした場合を考えます。
この場合は、オレンジの壁2枚、緑の壁1枚の合計3枚を通過するので
4個の立方体を通過します。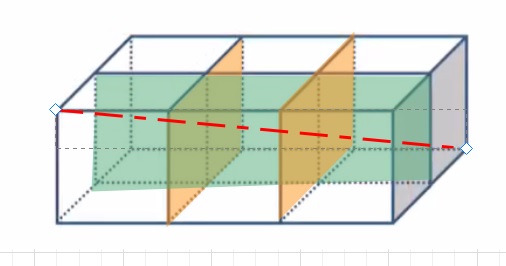
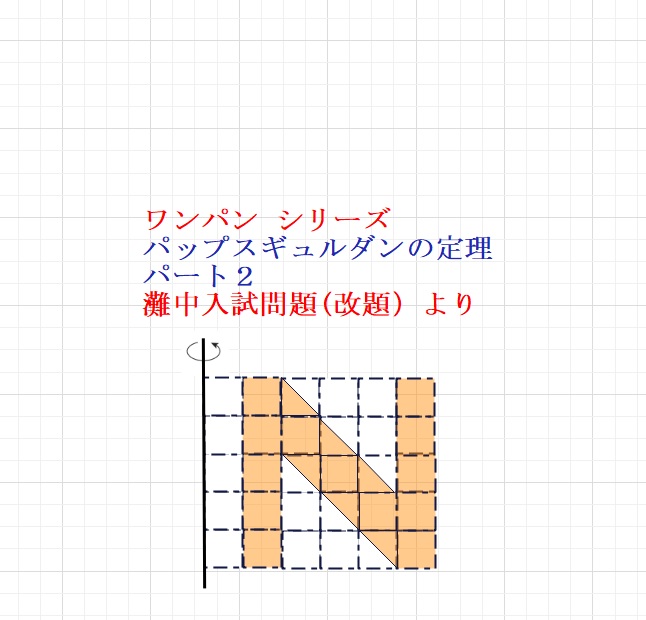
下図は、赤、オレンジ、緑の3枚の壁を通過しています。
よって4個の立方体を通過することになるはずですが、、
実際は、図のように2個の立方体をくしざしにしています。
それは、1度に3枚抜きをしているからです。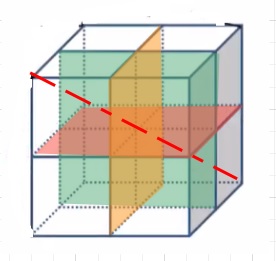
上図を縦、横、高さの3面からの分割で下図のように表すと、
分数の個数とつに抜ける壁の枚数が一致します。
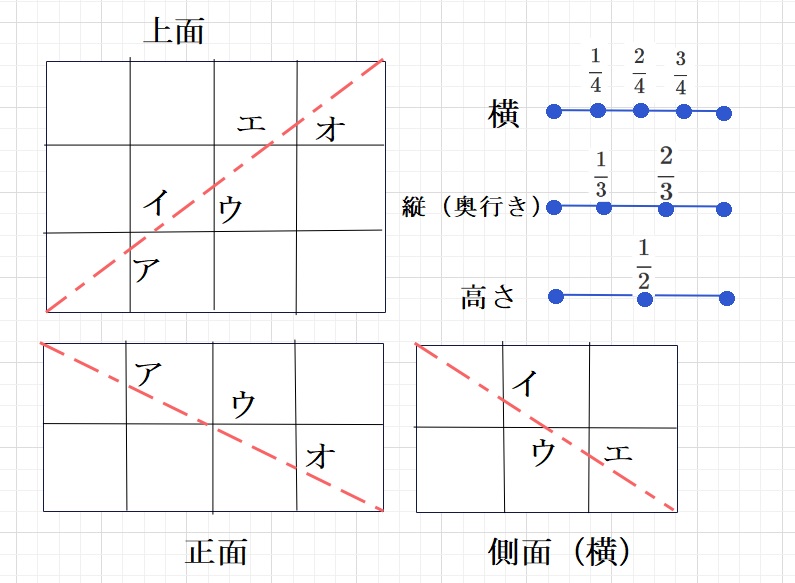
今回の問題を同様に縦、横、高さの3面からの分割で表すと、
下図のようになります。
【解答】

4と3と2の最小公倍数は12となります。
横)12を4等分すると、3となり、3,6,9となります。
縦)12を3等分すると、4となり、4,8となります。
高さ)12を2等分すると、6となり、 6となります。
よって、3,4,6,8,9の5個の壁を通過することとなり、
6個の立方体をくしざしにしています。・・・(答え)
コメント