難易度
2013年 算数オリンピック トライアル問題
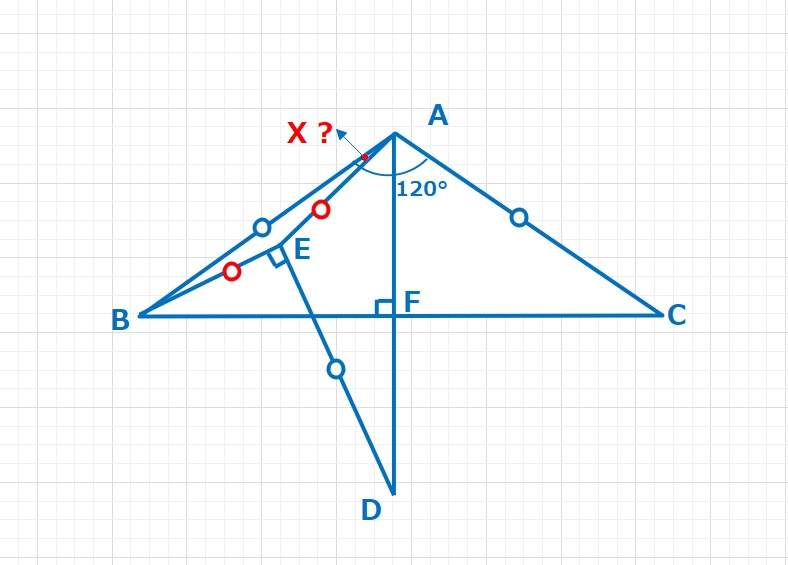
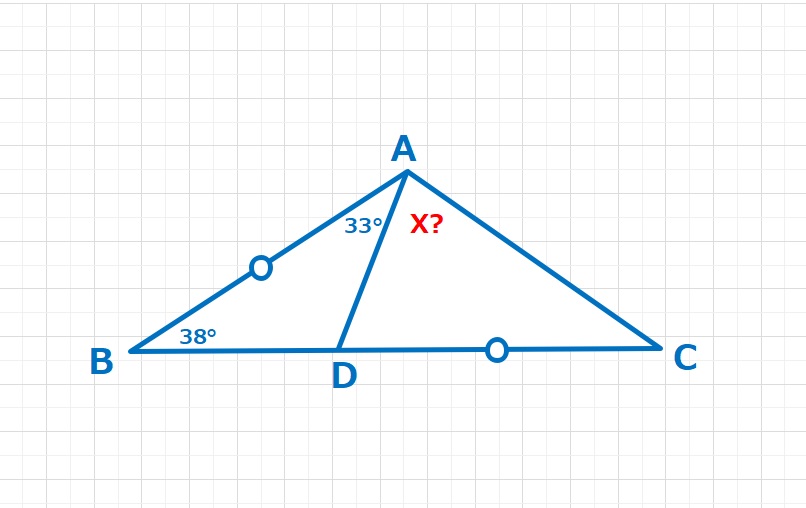
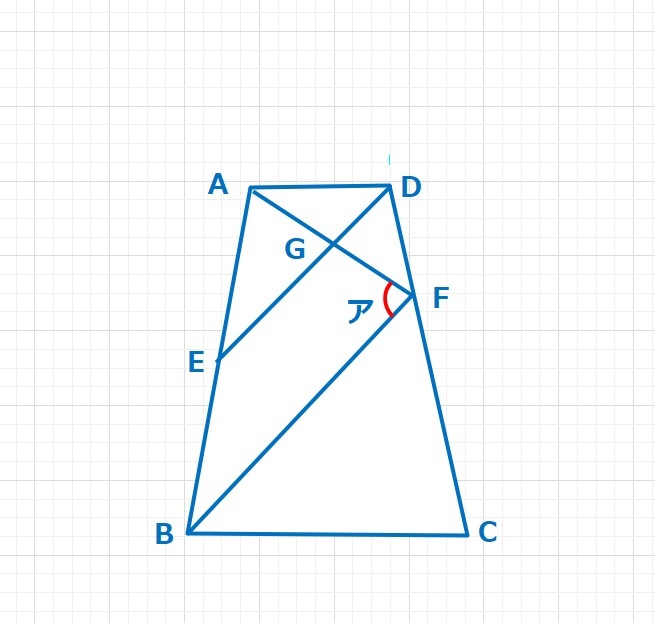
【問題】図において、AB=AC=ED, AE=BE,∠CAB=120°,∠AFC=∠BED=90°であるとき、X=∠BFEの大きさは何度ですか。
【ヒント1】左半分で十分なはずなのに、△AFCをわざわざ書いてくれているのが気になります。まず左右対称になるように図を書いてみて、AB=EDより二等辺三角形を移動させてみました。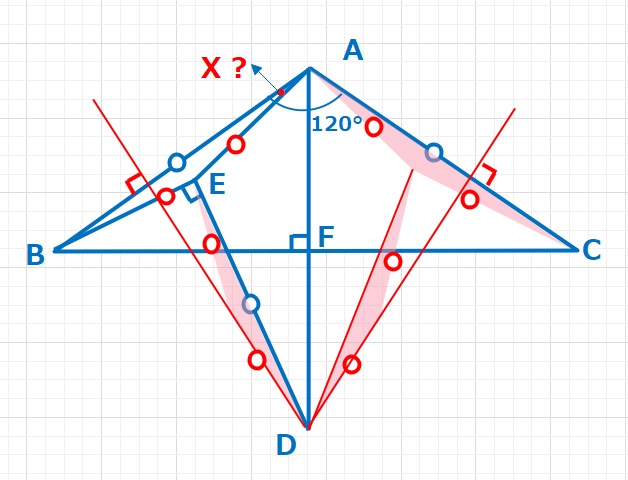
【ヒント2】△BIEと△DIFに注目すると、∠BEI=∠DFI=90°,∠BIE=∠DIFなので、∠EBI=∠FDI=30-Xとなります。また∠ABE=∠EDG=Xなので、∠FDG=30°となります。同様に∠FDH=30°となります。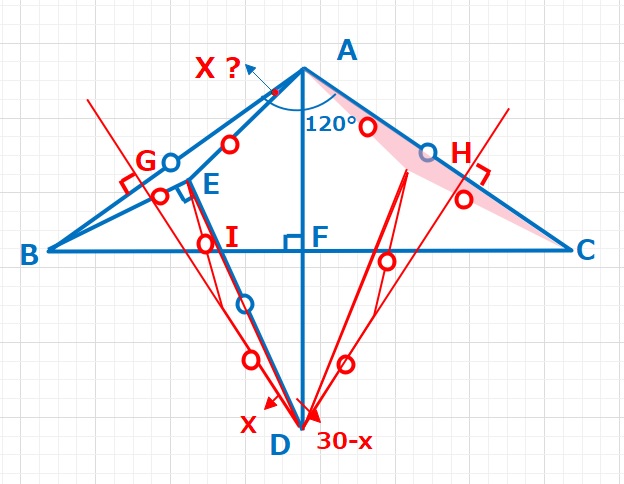
【解答】∠GDH=60°なので、△DJKは正三角形。よってDJ=DK=JK。またAE=EJ=JK=KL=LAなので五角形AEJKLは正五角形となります。よって∠LAE=108°となり、X=∠BAE=\(\displaystyle\frac{120-108}{2}\)=6°・・・(答え)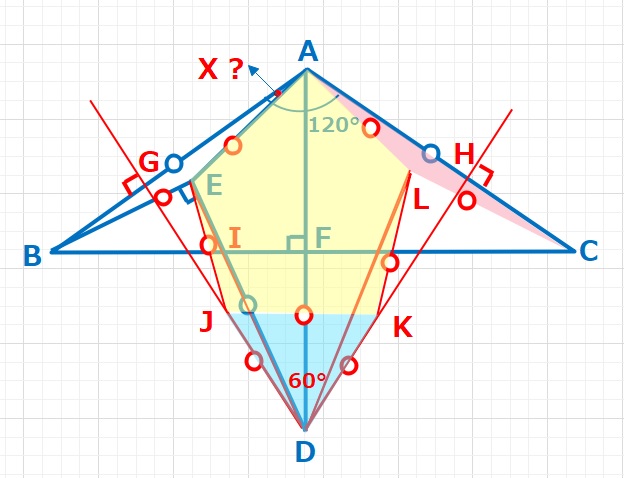
コメント