難易度
2007年算数オリンピック ファイナル
【ヒント】図形問題の基本は、自分で作図すること、そして対称性に注目し合同な図形を作ることです。今回の問題のように20°などの鋭角な問題は作図が難しく、イメージがつかみにくいですね(笑)
慣れるまでは、分度器と定規を使ってできる限り正確に作図するとよいと思います。
他の解説を見ると、もっと複雑な補助線をいれてるものしか見当たりませんが(笑)、下の図、すごくシンメトリーな図だと思いませんか。
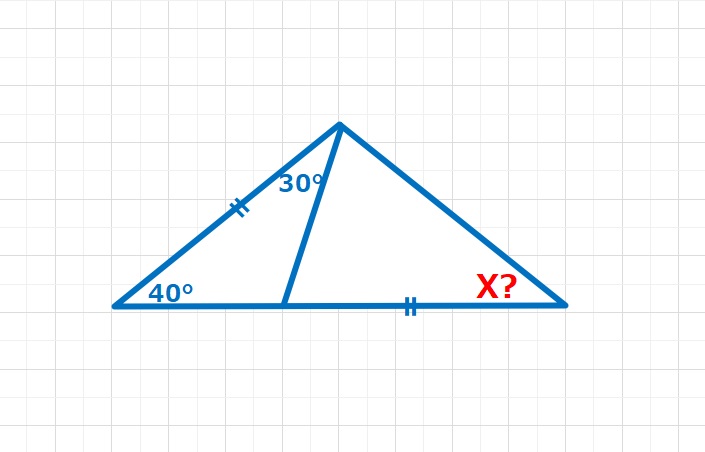
△ABCに注目して∠ABC=40°、∠BAC=100°より∠ACB=40°がわかります。つまり△ABCはAB=ACの二等辺三角形となります。最初にAHの垂線を引いてみました。∠CAH=∠BAH=50°となりますので、∠DAH=30°となり、ADを一辺とする正三角形AEDを作ってみました。だいぶ道筋が見えてきませんか?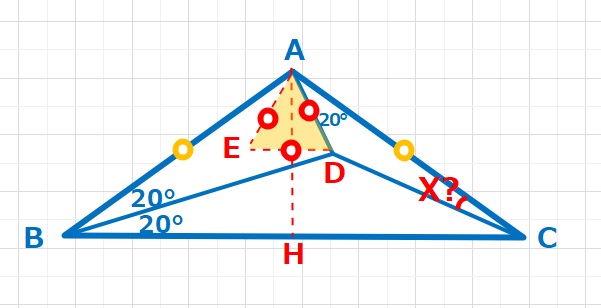
【解答】△CAEに注目すると∠ACE=20°、∠CAE=20+60=80°なので∠CEA=80°となり、△CAEは二等辺三角形となります。よってCA=CEとなります。また、△DAEは正三角形なので、DA=DEとなります。また、∠CAD=∠CED=20°なので、二辺とその間の角がひとしく、△CADと△CEDは合同な三角形となります。∠ACE=20°,∠ACD=∠ECDよりX=10°・・・(答え)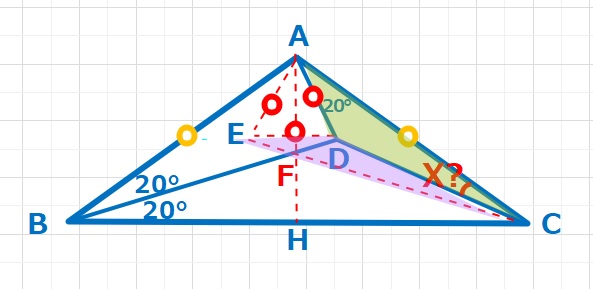
おまけ
下図のような大きな正三角形をさがすのが一般的なようです。難しい角度の問題では隠れた正三角形や二等辺三角形を探し出すことが大切ですので、慣れてる人は下のような補助線を引くことができます。
合同な三角形、△DBCと△EBCや△AECが∠EAC=40°が頂角の二等辺三角形であることに注目すれば解けそうですね。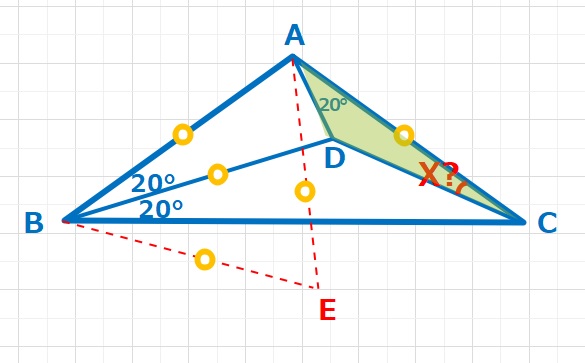
コメント