灘中 2020年入試問題より
【問題】上図のように数を並べたものがあります。各段の両端の数は１で、
2段目以降の両端以外の数は、その数の左上にある数と右上にある数の和になっています。
この100段目について、その一部（左から２つ、右から６つの数）をかくと、
1 100 ・・・・ 75287520 3921225 161700 4950 100 1 です。
また、11×11=121 ,11×11×11＝1331,11×11×11×11=14641
11×11×11×11×11=161051です。
以上のことを参考にすると、100個の11をかけた数、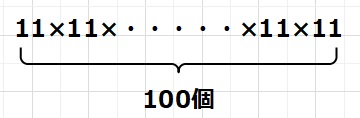
の下6ケタはいくつですか？
例えば、123456789の下6ケタは456789です。
【ヒント】この問題、背景をしらなくても、問題にすべてルールが説明されてますので、その場でルールを理解すれば、誰でも解けるようになっています。ただし、5分程度で解かなければいけません（笑）
11の倍数と三角形らしく広がっていく数の関係をみてみると、11を4回かけた数と4段目の数までは一致していますが、5段目は少し違うようです。
と微妙にちがいます。
これがどういうルールになっているかがわかれば解けます。
下3ケタ目は０になっていて、下4ケタ目が１になってることより、
10で１くり上がっています。
下3ケタ 10なので 下3ケタは０となり 次のケタへ１くり上がる。
下4ケタ 10とくり上がりの１で１１なので、
下4ケタは１となり、次のケタへ１くりあがる。
下5ケタ ５とくり上がりの１で６なので、下5ケタは６
下6ケタ １ となっています。
このルールがわかれば、あとは問題に答えが書いています。
【答え】
下１ケタ １
下2ケタ 100となってますので０となり100÷10＝10くり上がります。
下3ケタ 4950＋10＝4960となり、０で496くり上がります。
下4ケタ 161700＋496＝162196となり、６で16219くりあがります。
下5ケタ 3921225＋16219＝3937444となり、４で393744くりあがります。
下6ケタ 75287520＋393744＝75681264となり、４で7568126くり上がります。
よって下6ケタの答えは 446001・・・（答え）
【背景】この問題はパスカルの3角形とよばれるものがネタとなります。
パスカルの3角形は、色々な応用活用がされ、高校生数学レベルの範囲となりますが、
今回はその1例で、（１＋１０）を100回かけたときに、
10を100回かけた数の係数，10を99回かけた係数、・・・、10を2回かけた係数、10を1回かけた係数、１の係数が パスカルの3角形の100段目に左から順にあらわれるというものです。
これは、いいかえると、
1の位の数、十の位の数（10を1回かけた数）、百の位の数（10を2回かけた数）、千の位の数（10を3回かけた数）、万・・・の数を右から順に並べていること（私たちが日ごろ活用している十進数の計算をしていること）となります。
よって各位の数は1桁の数で表し、10を超えた数は次の位にくりあがるという計算
をすることなります。
今回の問題は、問題に書いているとおり11を100回かけた数は、パスカルの3角形を
使うことによって簡単に計算できることを教えてくれています。
係数も自分で計算することができますが、計算することが目的ではなく、考え方を理解できるか（メタ知識）を試す問題で、今回はすでに計算してくれているのだと思われます。
コメント