【問題1】18を連続する整数の和で表すと、何通りあるか。
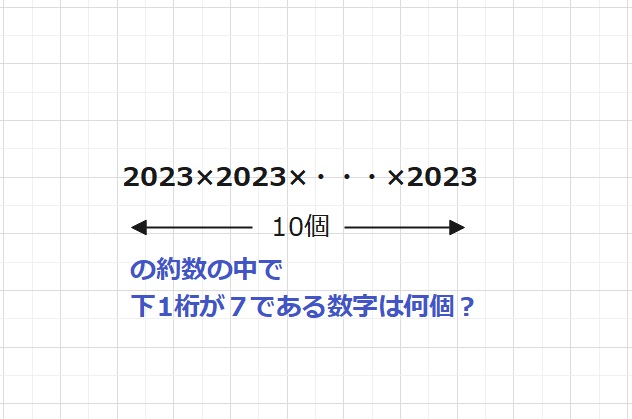
【問題2】2023を連続する整数の和で表すと何通りあるか。
またその整数のパターンは?
【問題1の解答】問題1を解くことが、問題2のヒントとなります。
18を連続する整数の和で表す方法を考えます。
(1)2つの連続する整数で表すとすると、18÷2=9が平均となります。2つの整数に分けることができそうにありません。
(2)3つの連続する整数で表すとすると、18÷3=6が平均となります。真ん中の数字が6なので、5,6,7となります。
(3)4つの連続する整数で表すとすると、18÷4=4.5が平均となります。
真ん中の数字が4.5はないので、連続する2数字のセットが9(4,5)を真ん中の数字とする2セットの数字でできていると考え、3,4,5,6となります。
(4)5つの連続する整数で表すと、18÷5=3.6が平均となり、
分けることができそうにありません。
(5)6コの連続する整数で表すと、18÷6=3が平均となります。
3が平均で6個の数字は3より小さい数字は1,2しかないので作ることができません。
連続する整数の和=①「平均」×「個数」若しくは②「連続した2数のセット」×「セット個数」
①のパターンは個数が奇数個のパターンで、②のパターンは個数はセットなので偶数個ですが、連続した2整数の和は必ず奇数になるので、どちらにしても奇数が入っていることとなります。
連続する整数の和は「その数の1を除く奇数の約数の数だけある」ことがわかっています。
これは知っていて損はないと思います。
今回の問題の場合、18の約数は1,18,2,9,3,6なので奇数の数、2通りあるとわかります。
3,4,5,6と 5,6,7の2通り・・・(答え)
【問題2の解答】2023=7×17×17となり、約数は1,7,17,119,289,2023の6通りあります。
よって連続する整数の和は5通りあることがわかります。
(1)2023=1×2023のパターンのとき連続する整数なので2セットの合計が2023と考え、
1011,1012 のセットとなり、これは合計2023になります。
(2)7×289の①のパターンのとき、289が平均でその前後に3つの数字がある、つまり
286~289~292の連続数となります。
②のパターンのとき、連続した2数のセットが289(144,145)を中心に7セットある、つまり 138~144,145~151の連続数となります。
(3)17×119の①のパターンのとき、119が平均でその前後に8個の数字がある、つまり
111~119~127の連続数となります。
②のパターンのとき、連続した2数の合計119(59,60)を中心に17セットある、つまり43~59,60~76の連続数となります。
1011、1012と286~289~292と138~144,145~151
と111~119~127と43~59,60~76の5通り・・(答え)

コメント