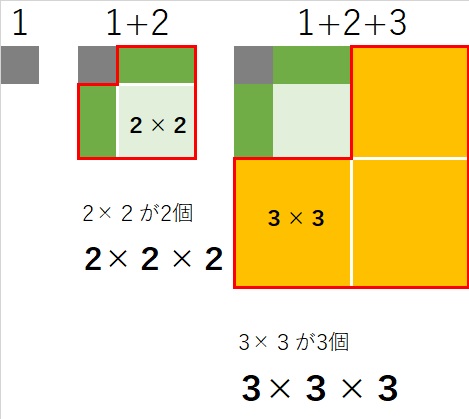
問題1 下図のように2×2×2は1辺が(1+2)の正方形から1辺が1の正方形を
除いた図形で表すことができる。2×2×2を2の立方数といいます。
3×3×3は1辺が(1+2+3)の正方形から、1辺が(1+2)の正方形を
除いた図形で表すことができる。
1×1×1+2×2×2+3×3×3+4×4×4+5×5×5は、
1辺がいくつの正方形で表すことができますか。
問題2 問題2 2025は5×5×3×3×3×3と表すことができることから、
2025=45×45であることが分かっています。
これを参考にして、2024を連続した立方数の和で表してください。
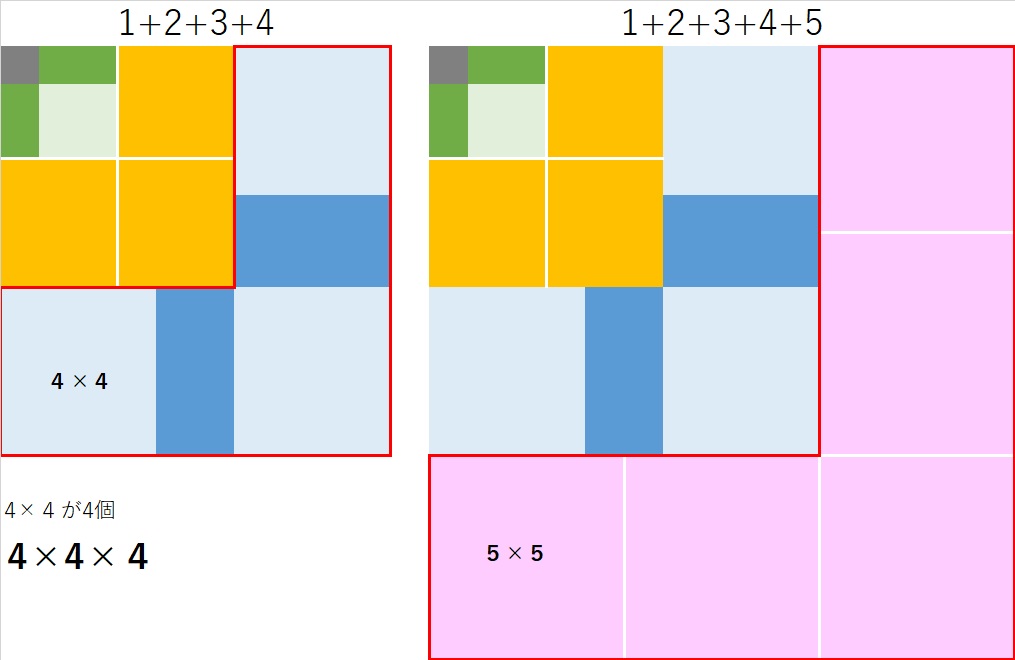
【問題1の答え】下図のように、1×1×1+2×2×2+3×3×3+4×4×4+5×5×5は
1辺が(1+2+3+4+5)=15の正方形で表すことができる。
【問題2の答え】
2025=45×45=(1+2+3+4+5+6+7+8+9)×(1+2+3+4+5+6+7+8+9)
と表すことができる。
つまり、1の立方数+2の立方数+・・・・+9の立方数で表すことができる。
2024=2025-1なので、
2024は 2×2×2+3×3×3+・・・+9×9×9で表すことができる。
よって、2024は 2から9までの立方数の和となる。 おわり



コメント