難易度
筑波大学付属中学入試問題
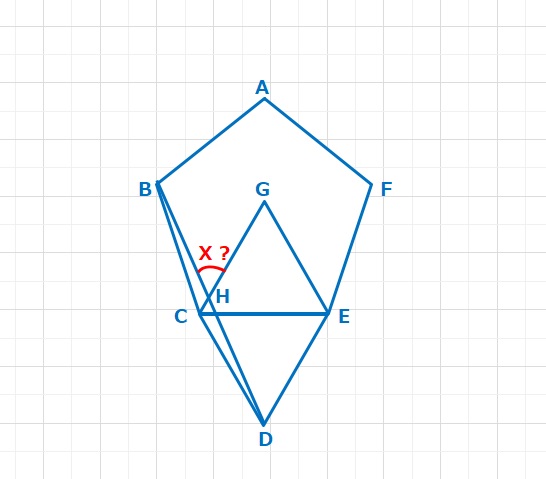
【問題】正五角形と正三角形を2つ組み合わせた図形があります。X=∠BHGの大きさは何度ですか。
【ヒント】基本に忠実に解いていけば簡単だと思います。正五角形の1つの内角は108°、正三角形の1つの内角は60°となるので、∠BCH=108-60=48°となります。
△CBDはCB=CDの二等辺三角形となります。∠BCH=108-60=48°となり∠BCD=48+60+60=168°です。よって∠CBD=\(\displaystyle\frac{180-168}{2}\)=6°となります。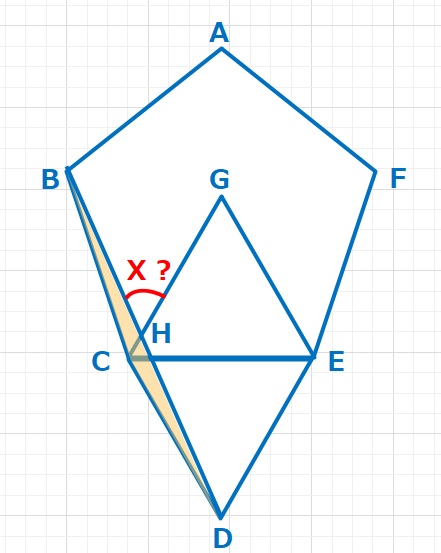
【解答】△HBCに注目して、∠HCB=48°,∠CBH=6°なので
X=∠BHG=∠HCB+∠CBH=48+6=54°・・・(答え)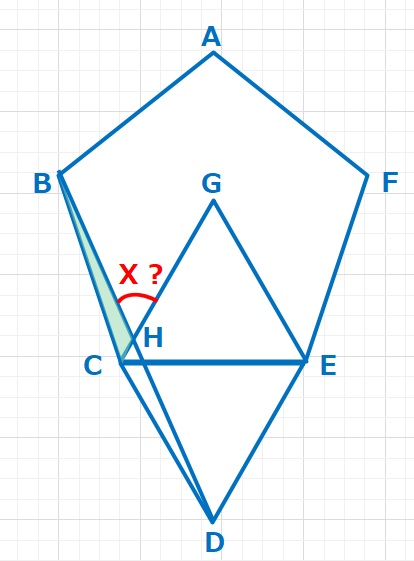
コメント