難易度
2018年 1日目 灘中入試問題より
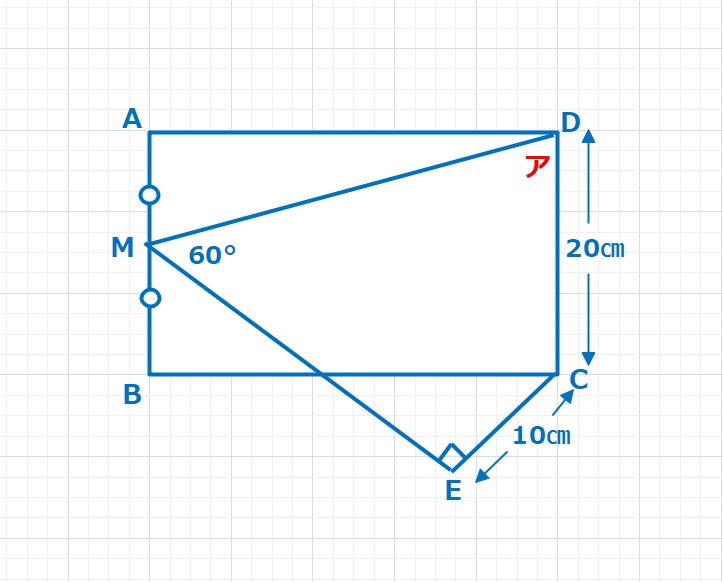
【問題】図で四角形ABCDは長方形で、辺ABの真ん中の点がMです。また、2本の直線CE,MEは垂直です。このとき、角アの大きさは何度ですか。
【ヒント】灘中の問題のなかでは簡単な方だと思います。まず、MからDCに垂線Lをおろしますと、DL=LC=10㎝となります。また∠DLM=∠CLM=90°です。感覚的に△MCLと△MCEは合同だとわかりますが、しっかりと確認する必要があります。△NMBと△NCEにおいて2角夾辺相当(∠NBM=∠NEC, ∠BMN=∠ECN,MB=EC=10㎝)なので合同な三角形です。∠MNB=∠CNE、「▲」+「×」=90°より、残りの角 ∠BMN=∠ECNが言えます。直角三角形の合同条件を使うとよいですが、忘れていれば、三角形の合同条件を使えばOKです。よってNM=NCがわかり、△NMCは二等辺三角形で、∠NMC=∠NCM=★となります。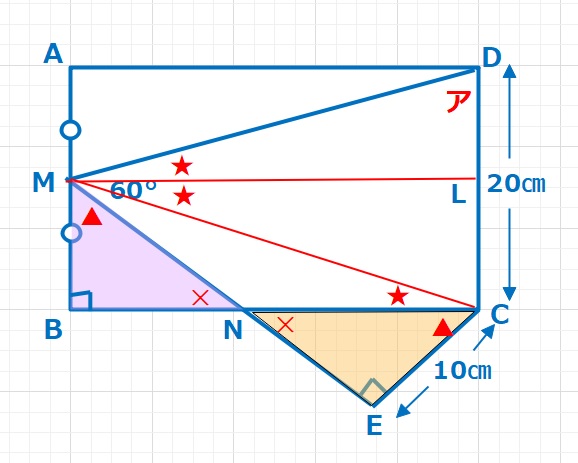
【解答】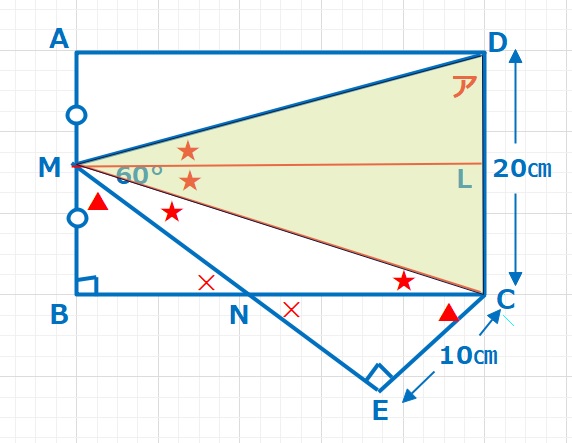
★★★=60°より ★★=40°となります。また△MCDは二等辺三角形なので、
ア=\(\displaystyle\frac{180-40}{2}\)=70°・・・(答え)

コメント