難易度
2017年 城北中学入試問題
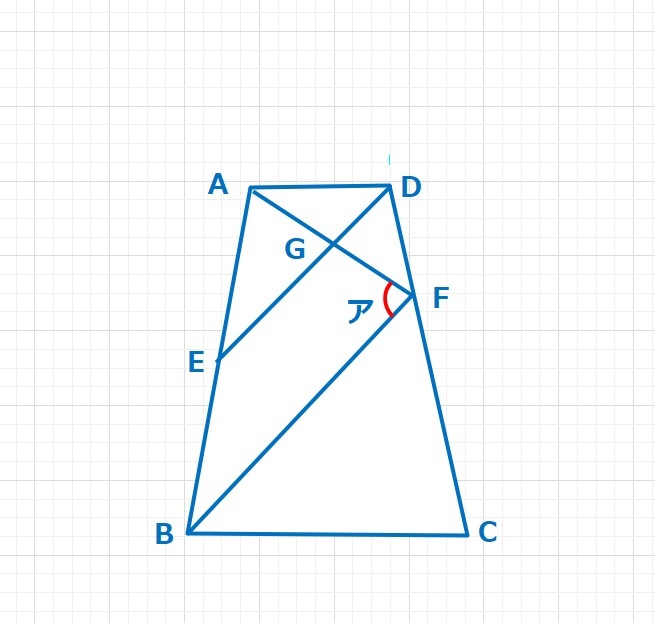
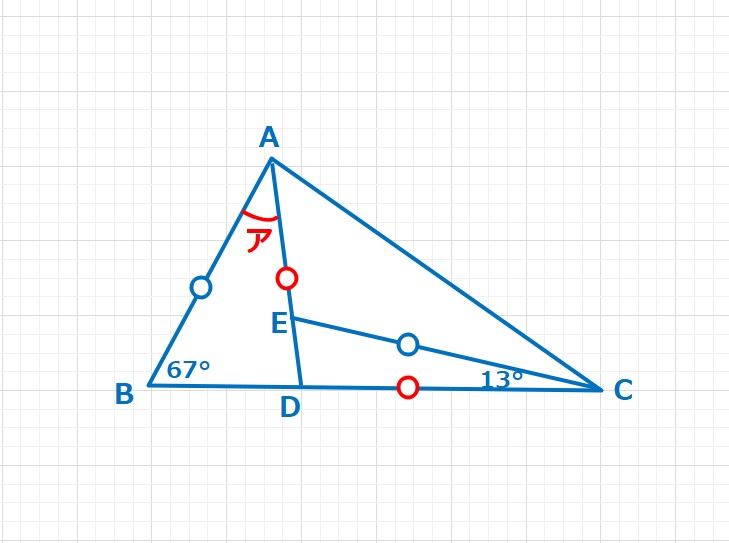
図の四角形ABCDはADとBCが平行な台形で、点Eは辺ABの真ん中の点です。DAとDF、CFとCBの長さがそれぞれ等しく、AFとDEの交わる点をGとします。
(1)角アの大きさは何度ですか。
(2)図の三角形AEGと三角形DGFの面積比が3:2のとき、長さの比DG:FBを求めなさい。
【(1)のヒント】
ADとBCは平行ですが、それと平行でFを通る線をひきABとの交点をHとします。DA=DFより△DAFは二等辺三角形なので、∠DAF=∠DFA。またCF=CBより△CFBは二等辺三角形なので、∠CFB=∠CBFです。ADとHFは平行ですので、∠DAF=HFA,HFとCBは平行ですので、∠HFB=∠CBFとなります。
図の●●▲▲は180°となります。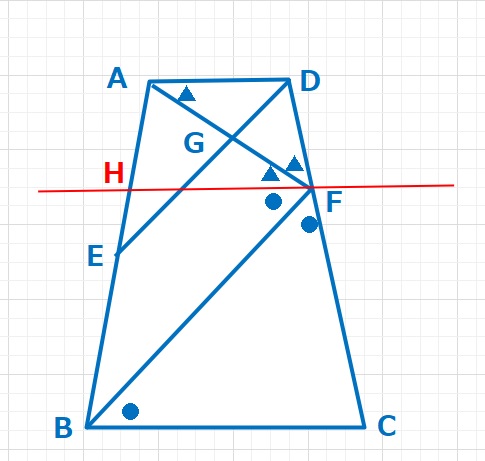
【(1)の解答】上図において ア=●▲=\(\displaystyle\frac{180}{2}\)=90°・・・(答え)
【(2)ヒント】
ADの延長線とBFの延長線の交点をIとします。△AEDと△ABIは相似な三角形となり、AE:EB=1:1なので、AD:DI=1:1,AG:GF=1:1です。また△GAEと△GDFの面積比は3:2で、AGとGFをそれぞれの三角形の底辺と考えると、∠AGE=90°なのでEGとGDはそれぞれの高さとなり、EG:GD=3:2となります。また、△AEGと△ABFも相似な三角形なので、EG:BF=1:2となります。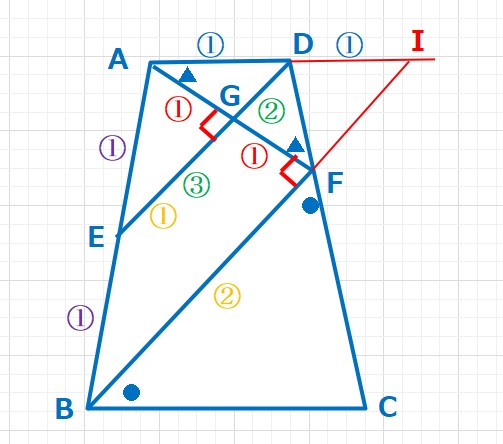
【(2)解答】EG:GF=1:2,EG:GD=3:2なので、DG:FB=2:6=1:3・・・(答え)
比の詳しい計算方法については別の場所で説明します。
コメント