難易度
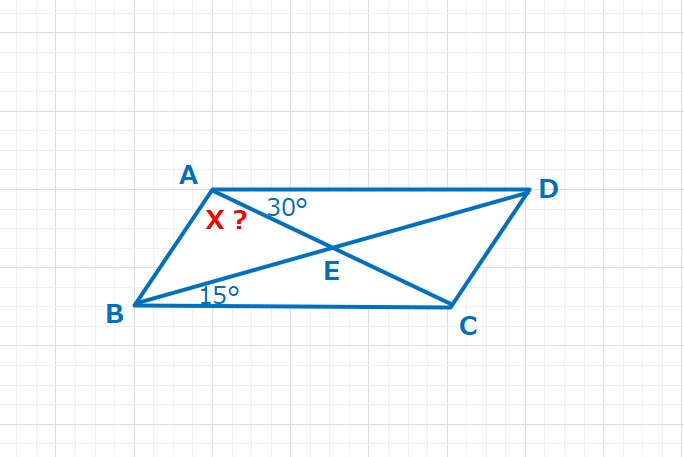
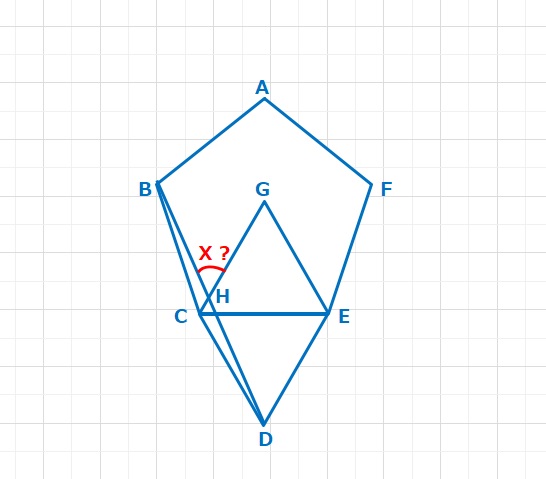
【問題】平行四辺形ABCDがあり、∠CAD=30°,∠DBC=15°のとき、X=∠BACは何度ですか。
【ヒント】ADとBCは平行ですので、∠DAC=∠ACB=30°に注目して、ACを1辺とする正三角形を作ります。平行四辺形の性質より対角線の交点はそれぞれの中点になるので、AE=ECであり、△AFEも正三角形となります。∠BFE=90°+60°=150°なので、△FBEに注目すると、∠FEB=180-(150+15)=15°となり、FE=FBの二等辺三角形ということがわかります。よってFB=FE=FAとなります。
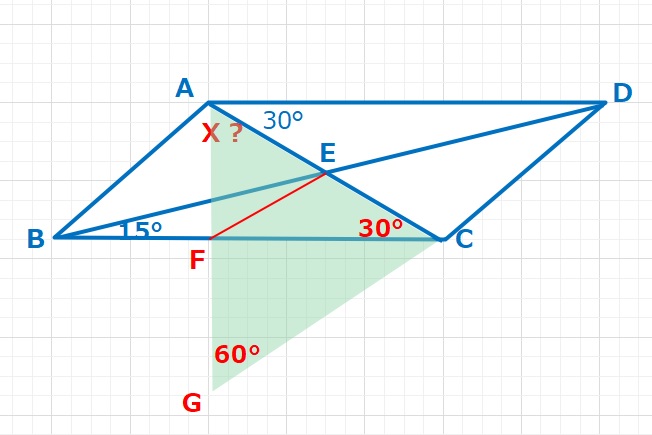
【解答】FB=FA, ∠BFA=90°より△FBAは直角二等辺三角形となります。よって∠BAF=45°。また△AFEは正三角形なので∠FAE=60°。 X=∠BAF+∠FAE=45+60=105°・・・(答え)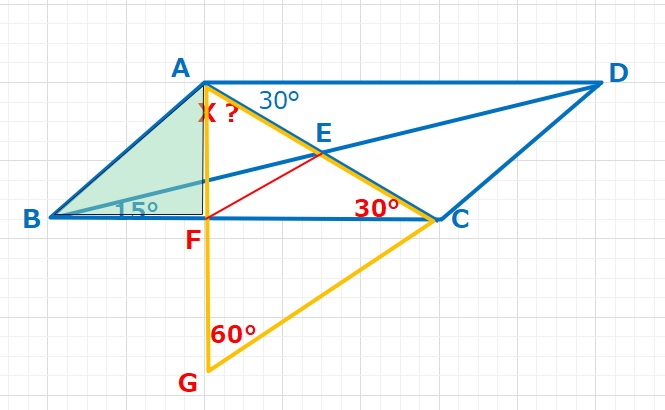
コメント