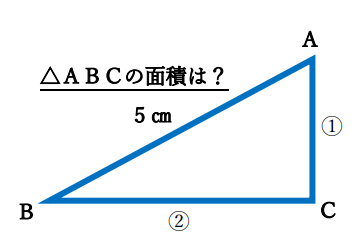
【問題】 直角三角形ABCがあります。斜辺AB=5㎝、短辺:長辺=1:2である△ABCの面積は何㎠ですか?
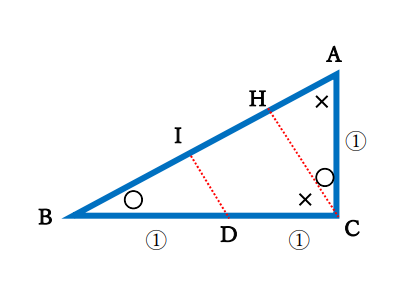
【ヒント】点Cから直線ABに垂線CHを引きます。またBCの中点をDとし、同様に点DからABに垂線DIをひきます。多くの相似な三角形が現れてきます。
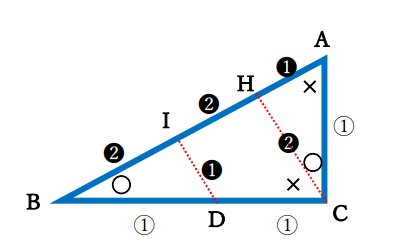
△AHCと△DIBは合同な三角形となり、△BDIと△BCHと△BACは相似な三角形となります。すべて直角三角形で短辺:長辺=1:2とわかってます。
【解答】直線AB=5㎝なので、直線CHは2㎝とわかります。
よって△ABCの面積はABを底辺と考えると、5×2÷2=5㎠・・・答え
これを一度解いたことがあるかないかで、試験で差がつきます!
中学生になってピタゴラスの定理を習えば一瞬なんですが、算数的な思考はとても重要です!

コメント