【コラム】ピタゴラスの定理とは？

みなさまピタゴラスの定理という言葉をきいたことがありますか？
ピタゴラスの定理は、別名､｢三平方の定理｣ともよばれている有名な証明済みの法則です。
証明済みの法則という言い方をしたのは、実はこの法則、ピタゴラスの生きていた紀元前
6世紀より前の古バビロニア（紀元前2千年頃）の粘土板の遺跡からつかわれていたことが
分かっているためです。
ピタゴラス以前に人々にとって、法則が本当に正しいのかを「証明」するという考え方が
なかったからだと言われています。
さて、そんなピタゴラスの定理とはどのようなものかを、まずみてみましょう。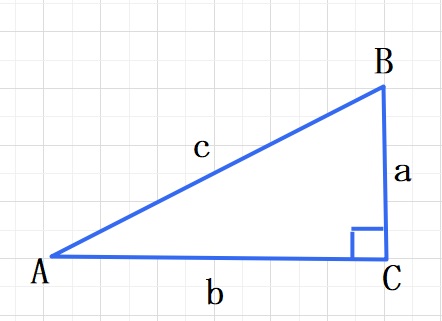

図のような直角三角形ABCがあり、それぞれの辺の長さをa,b,cとします。
このとき、　\(c^{2}\)=\(a^{2}\)+\(b^{2}\)　
ｃ×ｃ＝a×a+b×ｂが成り立つ、つまり
斜辺を2回かけた数字はその他の2辺a,bをそれぞれ2回かけた数字の和と等しくなる。
というものです。
この定理、ギネスブックのサイトでは520とおりの証明方法が発見されていると
書かれていて、これからもこの定理の注目度がわかると思います。

さてこの法則、ピタゴラス、正確にはピタゴラス教団は
どのようにして証明したのでしょうか。
諸説ありますが、ギリシャのサモス島で生まれたというピタゴラスは、
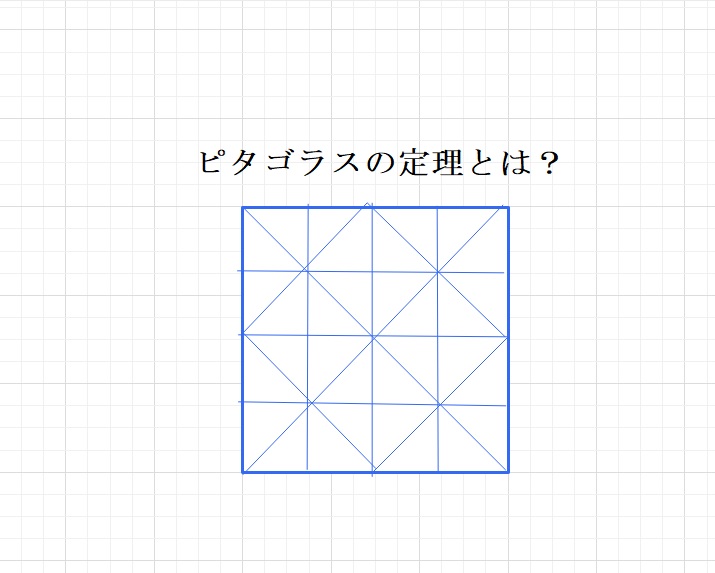
サモス島のヘーラー神殿を散策していたとき、足元に敷き詰められた
タイル貼り（下図）を見て、気づいたといわれています。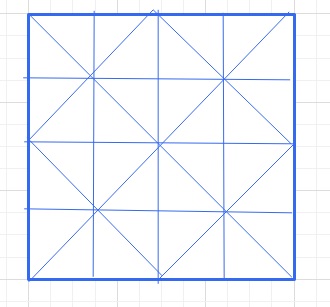

このタイルがピタゴラスには下のように見えたみたいです。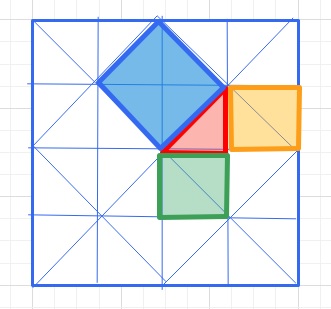

緑の正方形（直角三角形2個分）とオレンジの正方形（直角三角形2個分）の和が
青の正方形（直角三角形4個分）となっていることに気づいたそうです。
つまり式で表現すると、\(c^{2}\)=\(a^{2}\)+\(b^{2}\)　とうことですね。
ピタゴラスは、これをきっかけに一般化して証明を完成したということです。
こんな感じでしょうか。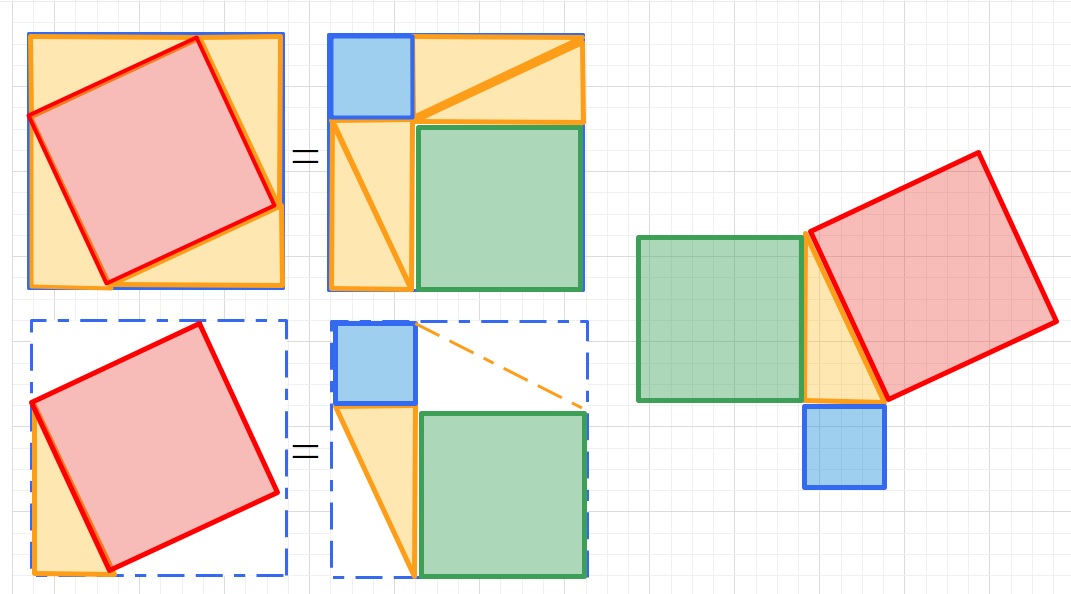

\(c^{2}\)=\(a^{2}\)+\(b^{2}\)
この式を満たす数字の組合せをピタゴラス数といいますが、ピタゴラスの時代には
3×３＋4×４＝5×５　や5×５＋12×12＝１３×13、7×７＋24×24＝25×25といった
基本的な組み合わせは経験的に知っていたようです。
この知識をきっかけにタイルをみてひらめいたのでしょうか（笑）
できすぎたお話しですね（笑）ちなみにピタゴラス数は無限にあります。
小学校では習いませんが、しっているととても便利なので、理解できたら
是非使ってみましょう。