古代エジプト人は分数を使うとき、いくつかの異なった単位分数(分子が1である分数)の和で表現しました。これをエジプト(式)分数といいます。この様子は、紀元前1650年前後の古代エジプトの数学文書であるリンド・パピルスで確認できます。しかし、なぜ単位分数の和で表現した本当の理由についてはいまだにわかっていません。ただし、リンド・パピルスには古代エジプト人がパンを分け合う問題がいくつも載っていて、その際このやり方が理にかなっていると思うことがよくあります。
例えば、「5個のパンを6人で分け合う」とき、どうすればよいでしょうか。
1人あたり、\(\displaystyle\frac{5}{6}\)であることはわかりますが、、、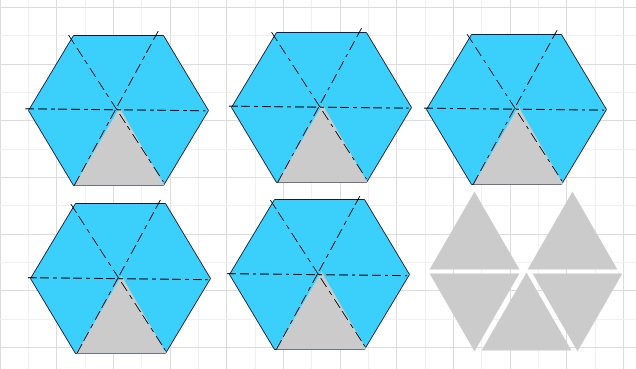
(実際6角形のパンがあるかどうかは別として)こんな分け方が一番らくそうです。
しかしこれでは、1人だけ余りの寄せ集めをもらった感じになってしまいませんか?(笑)
そこで、\(\displaystyle\frac{5}{6}\)=\(\displaystyle\frac{1}{2}\)+\(\displaystyle\frac{1}{3}\)とし、下図のようにわけると先ほどより公平な感じがします。
古代エジプト人はこの「分けやすさ」という日常での実用性にこだわっていたのかもしれません。
また、古代エジプトでは数字の位どりは10進法が使われ、10の7乗(10を7回かけた数字:千万)までの絵文字が確認されてます。(下図)
そして単位分数\(\displaystyle\frac{1}{n}\)を表すには、ヒエログリフ(神聖文字)では  をnにあたる数字の上において表現しました。
をnにあたる数字の上において表現しました。
例えば、\(\displaystyle\frac{1}{7}\)と\(\displaystyle\frac{1}{10}\)はそれぞれ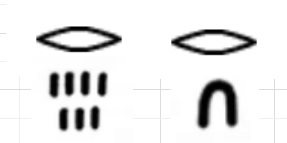 という感じです。
という感じです。
ただし、\(\displaystyle\frac{1}{2}\)は \(\displaystyle\frac{2}{3}\)は
\(\displaystyle\frac{2}{3}\)は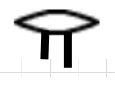 と、特別な記号で表したそうです。特に、\(\displaystyle\frac{2}{3}\)の左の短い棒は\(\displaystyle\frac{1}{2}\)を、右の長い棒は1を表し、合計\(\displaystyle\frac{3}{2}\)の上に
と、特別な記号で表したそうです。特に、\(\displaystyle\frac{2}{3}\)の左の短い棒は\(\displaystyle\frac{1}{2}\)を、右の長い棒は1を表し、合計\(\displaystyle\frac{3}{2}\)の上に を書き、逆数の\(\displaystyle\frac{2}{3}\)を表していました。
を書き、逆数の\(\displaystyle\frac{2}{3}\)を表していました。
古代エジプト人にとって\(\displaystyle\frac{1}{2}\)、特に\(\displaystyle\frac{2}{3}\)は、特別な存在だったと想像されます。
古代エジプトの絵文字には、ヒエログリフの他にヒエラティック(神官文字)とデモティック(民衆文字)と呼ばれる3種類の絵文字がありました。また、今回ご紹介したように、エジプト数学は日常の実用性を優先したがために、計算のロジックがシンプルではなく、数学の発展を妨げたともいわれています。とても興味深いはなしですね。
ヒエログリフ(神聖文字)による数字の表記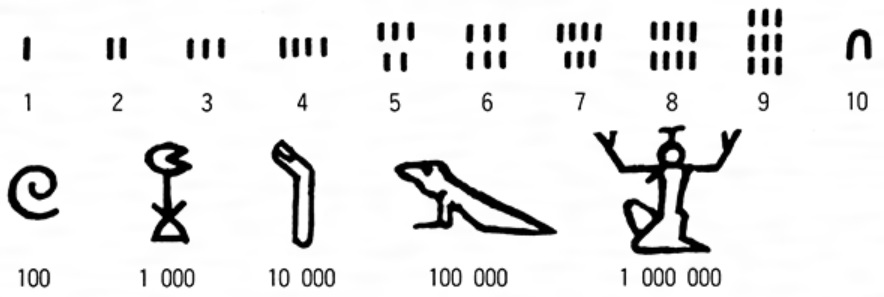
【コラム】エジプト分数の謎!
 コラム
コラム
コメント