立体の体積の求める際によく使うものとして、下の2つの公式があります。
(柱体の体積)=(底面積)×(高さ)
(すい体の体積)=(底面積)×(高さ)×\(\displaystyle\frac{1}{3}\)
柱体の体積は、限りなく薄い底面と同じ図形を上に積み重ねていく
イメージをすると理解できるかと思います。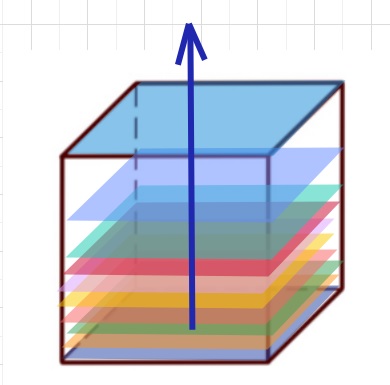
すい体の体積は、説明が難しいですが、一番シンプルな立法体で考えてみます。
今、下のような一辺が2㎝の立法体をかんがえます。立方体の中心と底面でできる四角すい
をイメージしてください。
この立方体は6個の側面を底面とする、青い四角すいと同じ四角すいでできていることが
イメージできますでしょうか。
立方体の体積は2×2×2=8、これを6等分したものが青い四角すいの体積ですので、
8×\(\displaystyle\frac{1}{6}\)=\(\displaystyle\frac{4}{3}\)となります。
青い四角すいの底面積は4、高さは1ですので、体積は(底面積)×(高さ)を
\(\displaystyle\frac{1}{3}\)倍していることがイメージできると思います。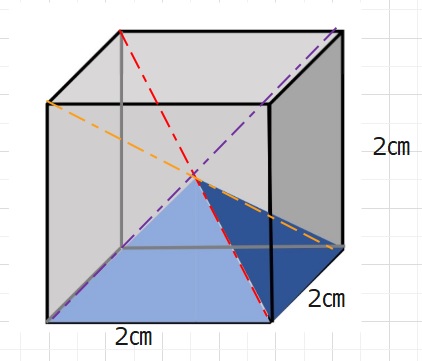
【裏ワザ】
その応用としてよく試験にでるのは、下のように切断した立体の体積を求める問題です。
この体積の求め方は、さきほどの柱の体積のイメージと似ていますが、限りなく薄い底面の図形を
重ねていくと、途中で形が変わっていきます。これは高さに依存してますので、高さの平均を
出してしまうという考え方です。少し論理的ではありませんが。
この考え方がつかえるのは、金太郎あめをイメージし、金太郎あめの顔が壊れない範囲の切断
をイメージするとよいと思います。これも伝わりにくいですね。
具体的に計算してみますと、
(左の体積)=(底面積)×(高さ平均)=(6×6)×\(\displaystyle\frac{2+4+5+7}{4}\)
(右の体積)=(低面積)×(高さ平均)=\(\displaystyle\frac{3×4}{2}\)×\(\displaystyle\frac{1+3+5}{3}\)
となります。
(おまけ)先ほどの四角すいの体積をこの裏ワザを応用して計算してみます。
垂直な高さがとれるような底面をさがし、三角形EACを底面とします。
三角形EACのACの長さをaとすると、EG=1㎝なので面積は\(\displaystyle\frac{a}{2}\)となります。よって三角すいEABCDの体積は
三角形EACの面積×(DB+A+C)×\(\displaystyle\frac{1}{3}\)
=\(\displaystyle\frac{a}{2}\)×\(\displaystyle\frac{a+0+0}{3}\)
=\(\displaystyle\frac{a×a}{6}\)
これも裏ワザとなりますが、直角三角形BACの∠ABC=90 °のとき
AB×AB+BC×BC=AC×ACが成り立ちます。よって4+4=a×aがなりたち
三角すいの体積は\(\displaystyle\frac{a×a}{6}\)=\(\displaystyle\frac{8}{6}\)=\(\displaystyle\frac{4}{3}\)となります。
この三角すいの体積の求め方もたまに試験のときに活躍します。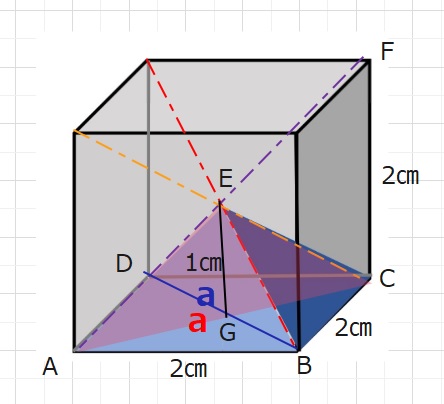



コメント