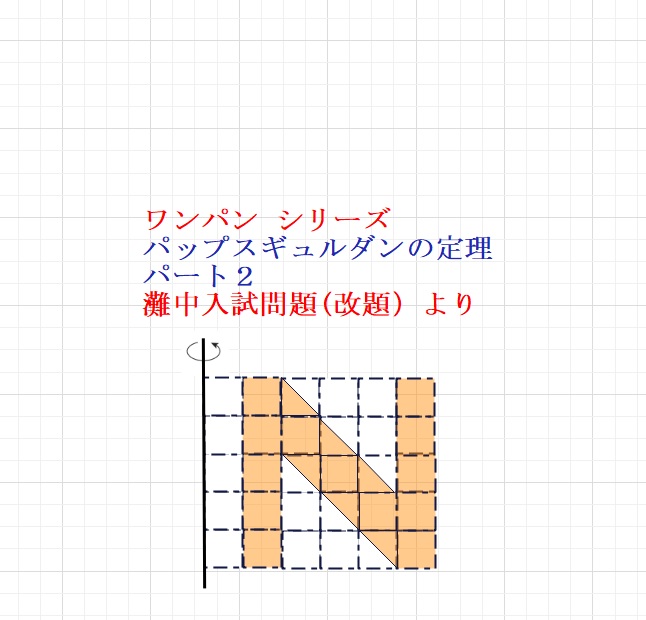
【例題】図のような、1目盛りの幅が1㎝の方眼用紙があります。
オレンジ部分の図形を、下図の軸を中心に一回転させたとき、
その図形が通過する部分の体積はア㎠です。
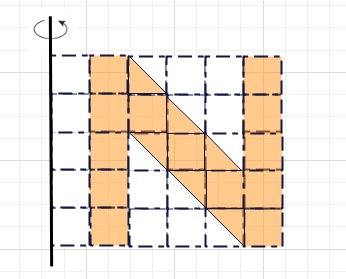
【ヒント】
前回ご紹介した、パップス・ギュルダンの定理をもう少し掘り下げてます。
こちらもご参照ください、ゼロから始める 図形問題の武器10 パップス・ギュルダンの定理 | 算数コロシアム (mathcolo.com)
「パップス・ギュルダンの定理」、なんか言いたくなりますのは私だけでしょうか(笑)
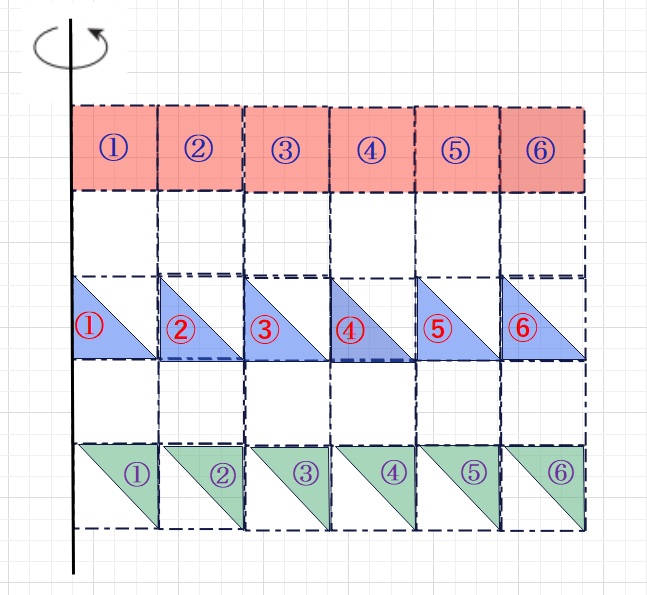
今、下図のような形を回転したそれぞれ回転した体積について考えます。
すべての基本となるものが、赤の正方形の①(軸にくっついているもの)の回転体の
体積となります。
①この体積は、パップス・ギュルダンの定理より、面積が1×1㎠で、重心は
軸より\(\displaystyle\frac{1}{2}\)㎝離れてますので、
1×2×\(\displaystyle\frac{1}{2}\)×3.14=3.14㎤となります。これが基本となります。
赤の正方形②は重心が1+\(\displaystyle\frac{1}{2}\)=\(\displaystyle\frac{3}{2}\)離れてます。
よって1×2×\(\displaystyle\frac{3}{2}\)×3.14=3×3.14と基本の3倍になります。
同様に、③④⑤⑥は軸から\(\displaystyle\frac{5}{2}\) \(\displaystyle\frac{7}{2}\) \(\displaystyle\frac{9}{2}\) \(\displaystyle\frac{11}{2}\) 離れてますので、
基本の体積(3.14)の5,7,9,11倍になることがわかります。
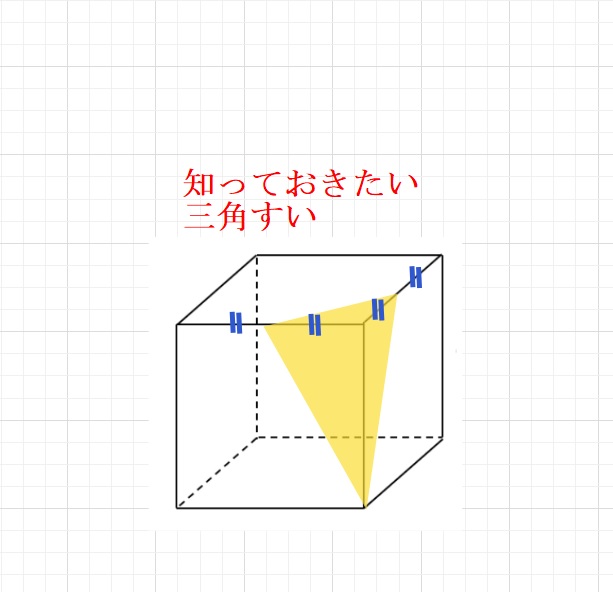
次に青の①の体積は、面積が1×1×\(\displaystyle\frac{1}{2}\) ,重心は\(\displaystyle\frac{1}{3}\)㎝離れてますので、
1×1×\(\displaystyle\frac{1}{2}\) ×2×\(\displaystyle\frac{1}{3}\)×3.14= \(\displaystyle\frac{1}{3}\)×3.14 ㎤となります。
これは最初の基本の図形の体積の\(\displaystyle\frac{1}{3}\)倍ですね。
ちなみに、緑の回転は緑と青をあわせて赤ですので、
1-\(\displaystyle\frac{1}{3}\)=\(\displaystyle\frac{2}{3}\)㎤となり、基本の\(\displaystyle\frac{2}{3}\)倍です。
青の②は軸から重心が1+\(\displaystyle\frac{1}{3}\) つまり\(\displaystyle\frac{4}{3}\)離れてますので、基本の\(\displaystyle\frac{4}{3}\)倍です。
同様に③④⑤⑥は1つ前の図形に1㎝たしたものが軸からの離れた距離なので、
\(\displaystyle\frac{7}{3}\) \(\displaystyle\frac{10}{3}\) \(\displaystyle\frac{13}{3}\) \(\displaystyle\frac{16}{3}\)倍となります。
残りの緑は、青を参考に\(\displaystyle\frac{2}{3}\) \(\displaystyle\frac{5}{3}\) \(\displaystyle\frac{8}{3}\) \(\displaystyle\frac{11}{3}\) \(\displaystyle\frac{14}{3}\) \(\displaystyle\frac{17}{3}\)倍となります。
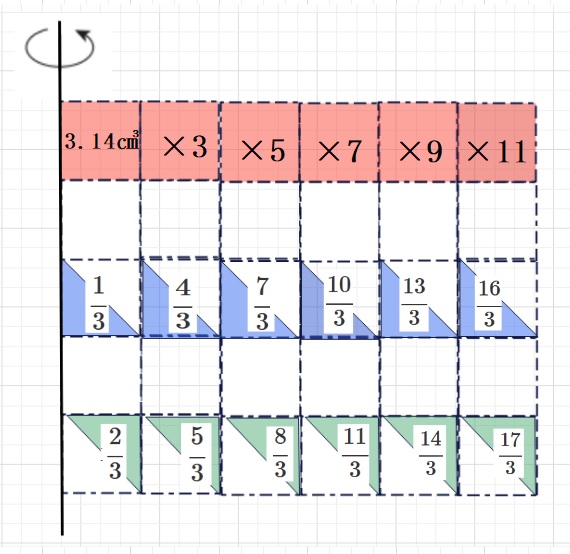
【まとめ】1㎝の正方形を軸を中心に回転した体積は、
基本形(軸にひっついている)は3.14㎤となり。
それを基準に 下図のような倍率になります。
離れた距離が同じならば、もちろん赤=青+緑になってますね。
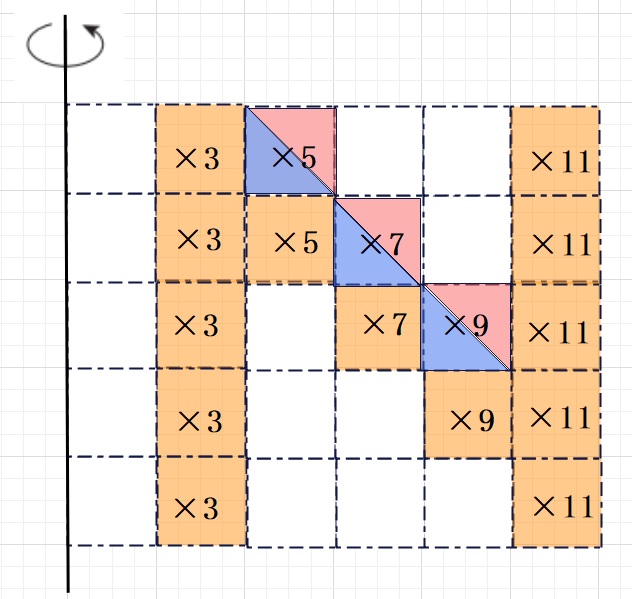
【解答】少しだけ、問題の図をわかりやすくしました。
下の図より 3倍が5個、5倍、7倍、9倍が2個ずつ、11倍が5個より
3×5+(5+7+9)×2+11×5=15+42+55=112
基本形が3.14なので、ア=112×3.14=351.68㎤・・・(答え)
コメント