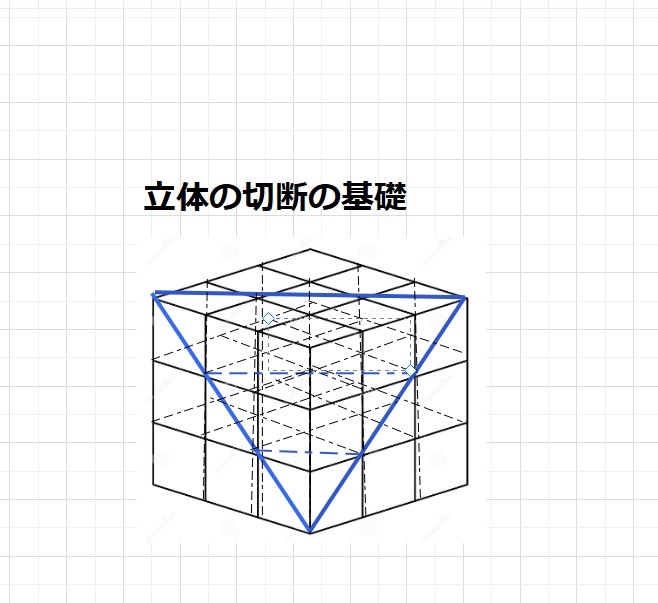
立方体や直方体の切り口を見つけるには3つのルールを活用します。
これは理解できるまで何度も練習してほしいです。
ルール1.同じ面上(平面上)の2点は結ぶ。
ルール2.平行な面の切り口は平行になる。
ルール3.面をのばす。
ルール1のみで解けるパターン。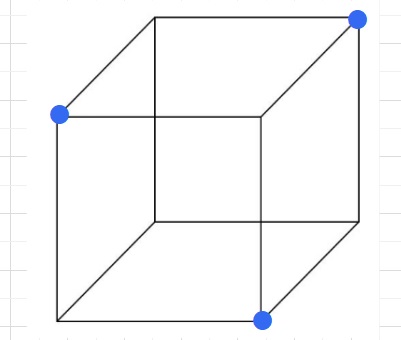
点Aと点Bは緑の平面上にあるのでルール1より2点を結びます。
点Bと点Cは赤の平面上にあるのでルール1より2点を結びます。
点Cと点Aは青の平面上にあるのでルール1より2点を結びます。
以上により、切り口ができました。切り口は正三角形であることがわかります。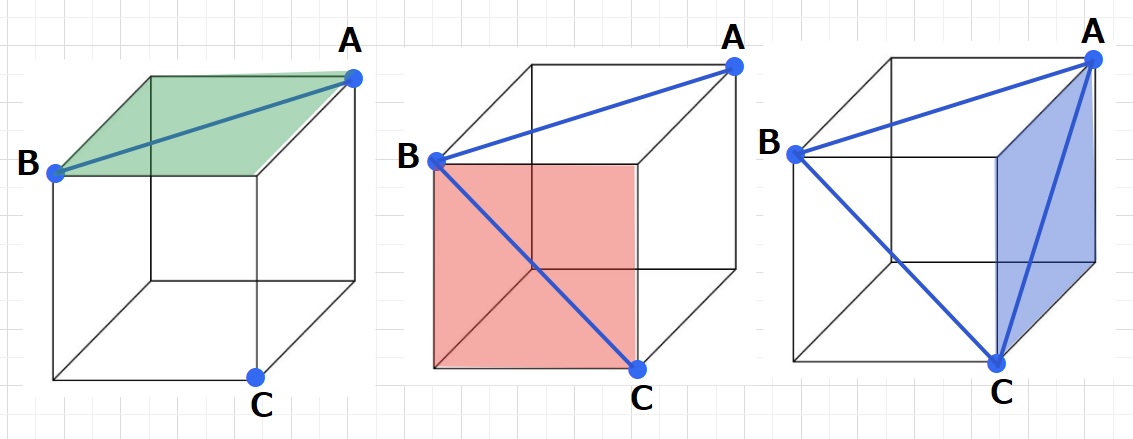
ルール1とルール2を使うパターン。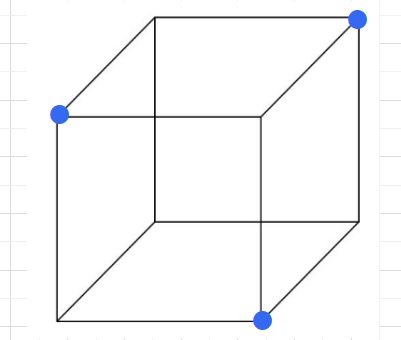
ルール1を活用し、緑と赤の平面上にある点Aと点B、点Bと点Cをそれぞれ結びます。
ルール2より、平行な青い面の切り口は平行になるので、
線分BCに平行になる線分ADをつくります。
あとはルール1を使い、黄色い平面上にある点Dと点Cをむすべば切り口の完成です。
切り口は等脚台形となりました。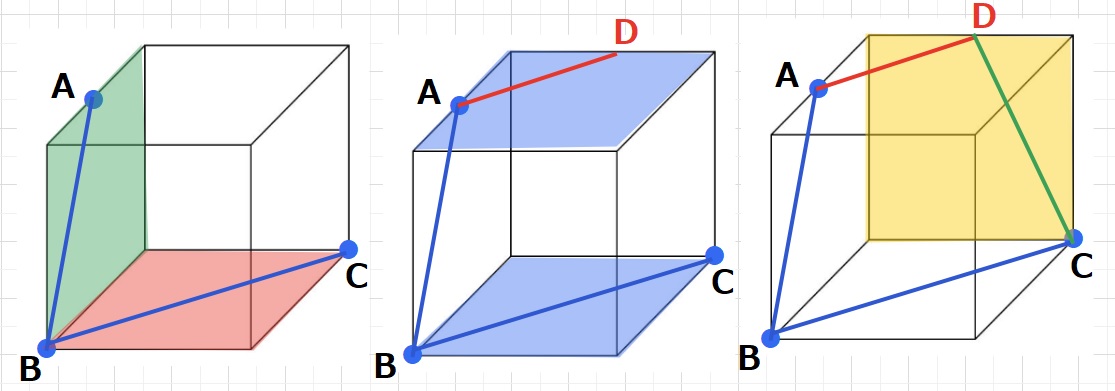
ルール1・2・3を使うパターン。
ルール1より青と黄色の平面上の点Aと点B、点Bと点Cを結びます。
ここでルール1もルール2も使えずに行き詰まりますので、ルール3を使います。
ルール3より青の面をのばし、線分ABものばし点Dを作ります。
ルール2より平行な黄色の面の切り口は平行になるので点E,点Fができます。
ルール1より点Aと点Eをむすびます。
ルール2より線分AEと平行な線分CGを作ります。
ルール1より点Gと点Fを結びます やっと切り口が完成しました!
点A,B,Cがそれぞれの線の中点とすると、切り口は正六角形となります。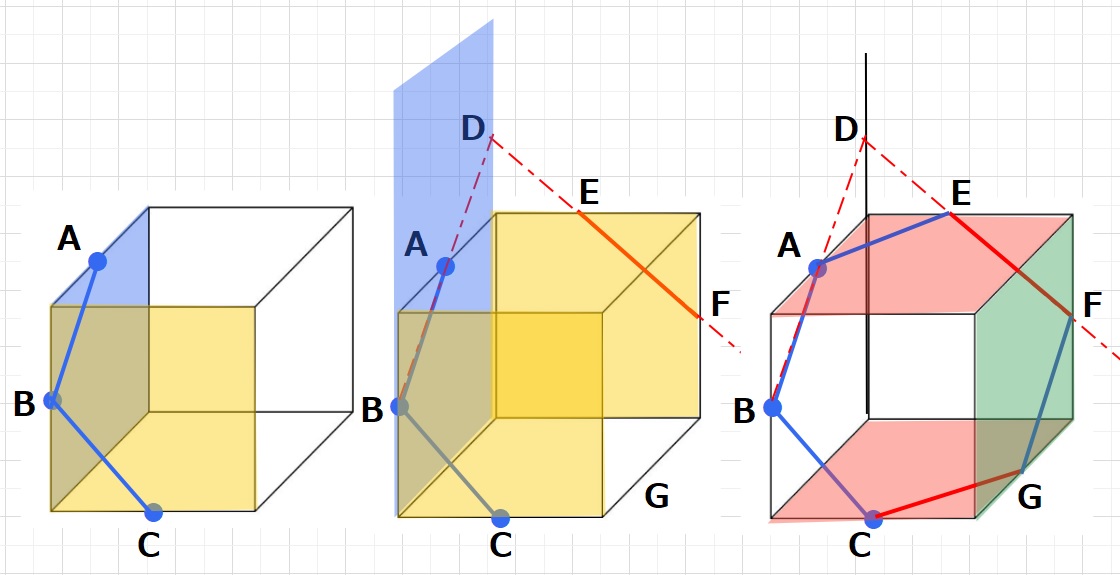
おまけで、もうひとつルール1とルール2でとける5角形となるパターンを
簡単に紹介します。
ほかにも正方形、長方形、ひし形、平行四辺形、二等辺三角形、(台形、六角形)
など色々な切り口ができますので、考えてみてください。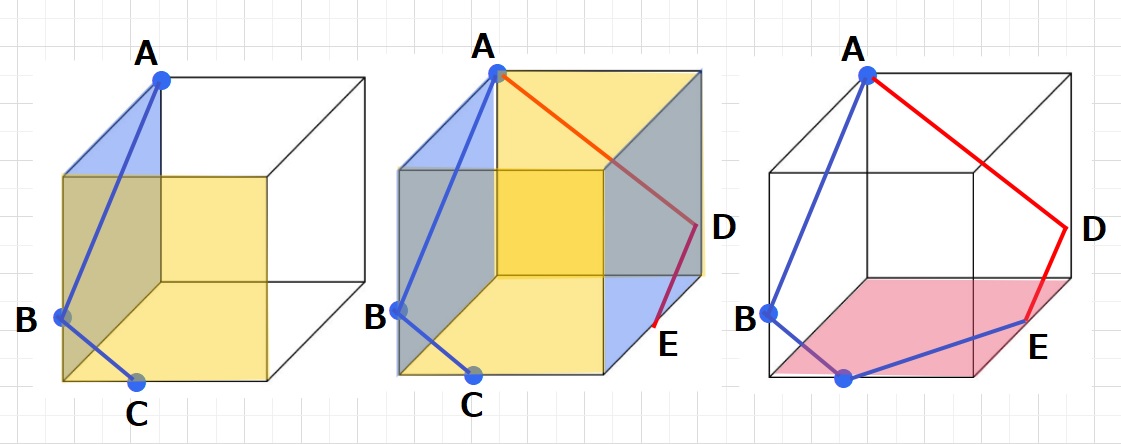
次に立方体を積み上げて作った大きな立方体を切断する場合についてみていきます。
切断される断面や小さな立方体の個数は、
大きな立方体を水平面方向に切り分けた断面図で把握できます。
今、図のような青線部分で3×3×3の小さい立方体を
積み上げてできた大きな立方体を切断します。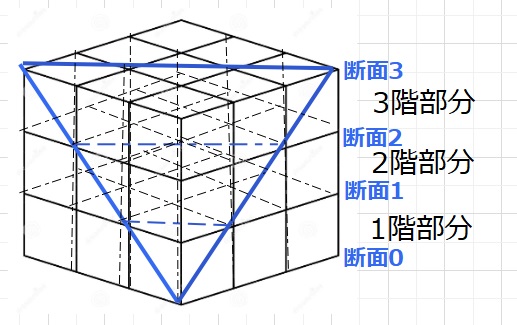
1階部分の断面は断面0と断面1で判断できます。
同様に、2(3)階部正の断面は、断面1(2)と、断面2(3)で判断できます。
よって切断される立方体の個数は9個とわかります。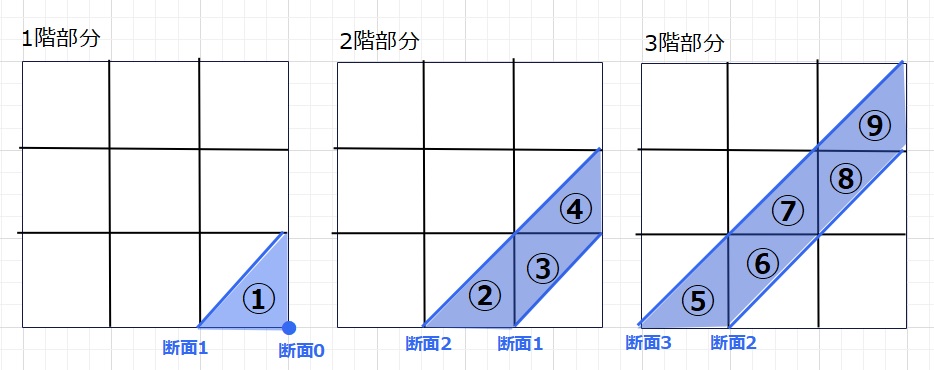
また、断面図は下図のような正三角形となります。
以上のように水平面で切った断面により概略を把握し、実際の断面図とあわせて
総合的に判断すると把握できます。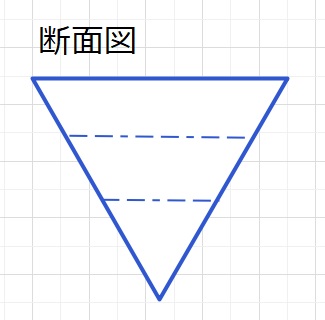
コメント