同じ数のかけ算の工夫
【例題】47×47を 考えてみます。
これも、いつもどおり面積で考えます。47をきりのよい40と7にわけると、
47×47の面積は 青色部分(40×40)と紫部分(40×7)が2個と黄色部分(7×7)
の合計を求めるのと同じになります。
なれると、ほぼ暗算で計算できます。
平方数は色々なところで使いますので、絶対にみにつけておきましょう。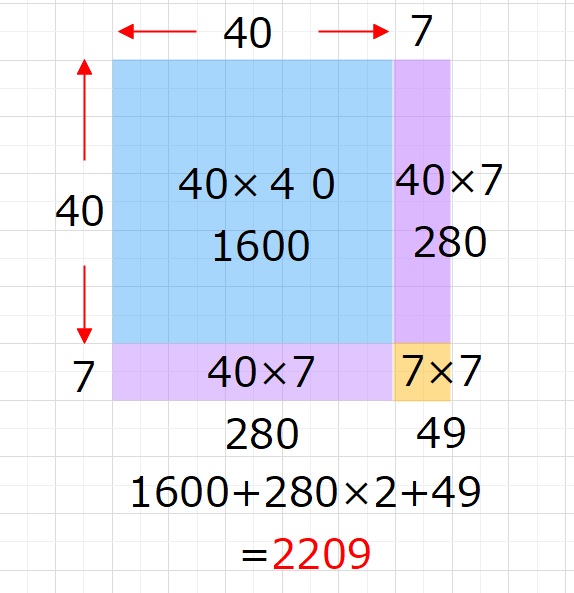
もう少し考えてみましょう。
青色の面積は3ケタ目の数を計算しています。
また黄色の面積は1ケタの数を計算しています。
この合計はすぐ計算できると思います。今回の例でいうと47×47の
4×4を計算した16をそのまま書く。そして7×7を計算した49をつづけて書いた数は、
1649となります。これが青と黄色の合計面積です。
たとえば 21×21ですと 2×2=4と1×1で401ですね。これ1と書かずに01と書くことをわすれないように。(笑)
話がそれましたが、47×47の場合は、1649に紫色の2ケタめの数をたすだけです。
紫色の部分は14×40=560ですので、1649+560の赤字の部分を計算して、2209ですね。
普通のひっ算をした方が早いと思う人もいるかもですが、数字によってはこの考え方で計算した方が早い時があります。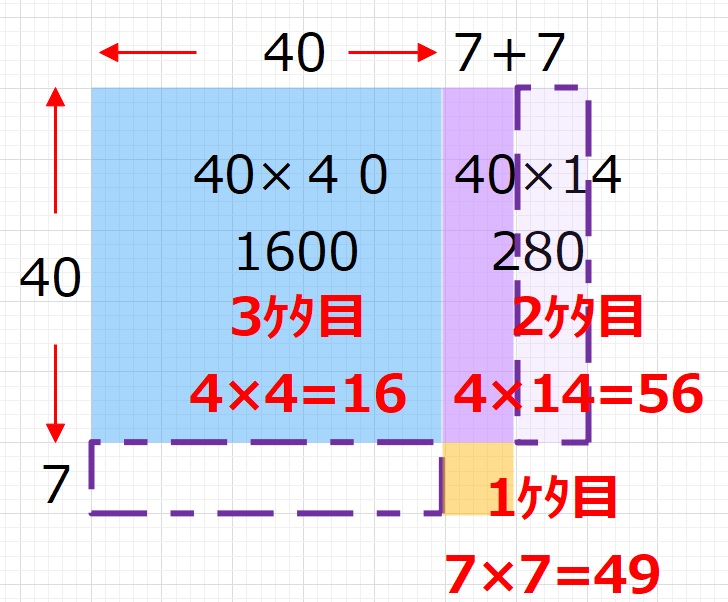
2ケタ目の数字が同じで、1桁目の数字の合計が10になる2ケタかけ算
もう少し発展させて、この考え方が得するパターンをさがしてみます。
2ケタ目の数字が同じ数字で、1ケタの数字の合計が10になるパターンです。
例えば、43×47のようなパターンです。
このパターンの場合 (2ケタ目の数)×(2ケタ目の数+1)を計算、今回は
4×5=20。これに1ケタめの数のかけ算 3×7=21をつづけて書いた2021、
これが答えになります。考え方は下のとおりです。
条件が限定されますが、これはかなり楽ですね。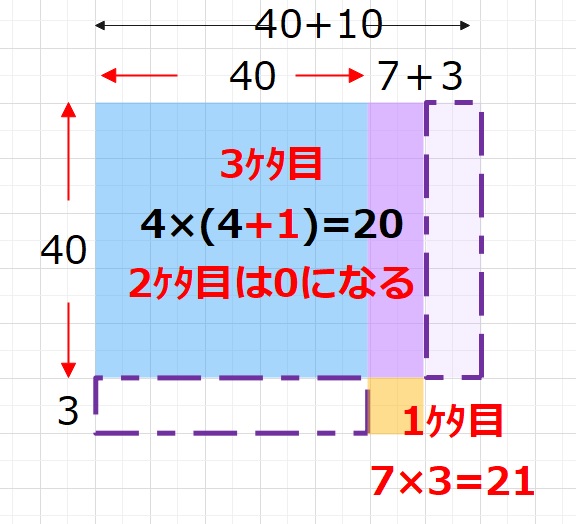



コメント