周期算とは、ある規則で並んだ数字やマークの〇番目を求める問題です。
具体的な例をとおしてご紹介します。
【例題1】ある規則に沿って並んでいる数字
2,4,6,5,3,2,4,6,5,3,2,4,6,5,3,2,4,6,5,3,2,4,6・・・があります。
2023番目の数字はいくつですか。
【解説】このような問題はまず、規則性を見つけることが重要です。
じっくりみると、2,4,6,5,3を繰り返していることがわかります。
周期算では基本的に、①最初からの番号 ②周期内番号 ③周期番号で管理すると
スッキリします。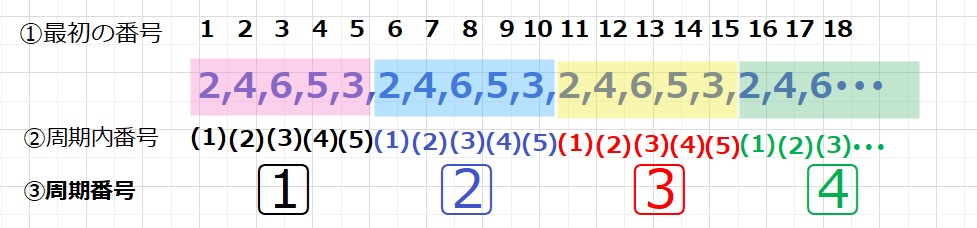
問題は①最初の番号が2023番目ということなので、5を周期として繰り返していることより、
2023÷5を計算します。2023÷5=404余り3となります。
よって2023は ③周期番号が 405番目 ②周期内番号が3番目の数字つまり
「6」・・・(答え)とわかります。
【例題2】2,4,6,5,3,2,4,6,5,3,2,4,6,5,3,2,4,6,5,3,2,4,6・・・があります。
順番に数字を足していき、2023よりはじめて大きくなる数字は何番目ですか。
【解説】これも例題1と同様ですね。
1周期の数字をすべてたすと、2+4+6+5+3=20になります。
2023÷20を計算すると 2023÷20=101余り3となります。
ということは101番目までたすと、2020になり、次の数字をたすと2020+2=2022
ですので、2023よりはじめて大きくなる数字は 2026で
103番目の数字・・・(答え) となります。
(参考1)累乗の1の位の数字のならびについて
今、3,3×3,3×3×3,3×3×3,3×3×3×3,3×3×3×3×3・・ の数字の並び方を考えてみると、
順番に 3,9,27,81,243,729,2187,6561,19683・・・となります。
下1桁の数字に注目すると、3,9,7,1,3,9となっており、1が出てきた時点で3をかけて最初の3に戻りますので同じ数字を繰り返すことがわかります。
つまり 3の累乗の1桁の数字は「3,9,7,1」を1周期として循環しています。
ご参考までに1ケタの整数の累乗の1の位をご紹介いたします。
1の累乗→「1」1,1,1,1…ずっと1(笑)
2の累乗→「2,4,8,6」「2,4,8,6」…
3の累乗→「3,9,7,1」「3,9,7,1」…
4の累乗→「4,6」「4,6」…
5の累乗→「5」5,5…ずっと5(笑)
6の累乗→「6」6,6…ずっと6
7の累乗→「7,9,3,1」「7,9,3,1」… 3の累乗に似てますね。
8の累乗→「8,4,2,6」「8,4,2,6」…
9の累乗→「9,1」「9,1」…
(参考2)循環小数について
循環小数とは、小数点以下のある桁から先で同じ数字の列が無限に繰り返される小数の
ことをいいます。
【例題3】 1÷14を計算した時、小数第2023位はいくつですか。
【解説】
実際に計算してみます。
1÷14=0.0714285714285・・と「714285」6個の数字を1周期として
循環することがわかります。
2023÷6=337余り1となりますので、
小数第1位の数字は0で小数第2位より循環していることより、
小数第2023(2022+1)位は5となります。・・(答え)

コメント