「場合の数」とは、「ある事柄が何とおり起こるかの総数」のことです。
もっと簡単に言うと「場合の数」は「起こると考えることができるすべての数」と同じ意味です。
たとえば、サイコロを1回振った時の場合の数は、6通りとなります。
場合の数を考えるとき重要なのは整理して考えることで、
自分でルールを作っておいて、それに基づいて仕分けすることです。
①もれなくダブりなくカウントする。
②複雑な場合は、小分けにしてグループ別に考えていく
③場合分けのパターンを少しでも減らすために、固定したり、まとめてペアにして減らしたりする
④多いパターンではなく、少ないパターンの方を数える
です。
場合の数や確率は日常生活と密接に関係してますので、身近な行動のなかで、
あてはめて考えてみると思考力が養われます。
順列と組合せ
場合の数には、1.順列と2.組合せの大きく2種類があります。
違いは、順番をきにするかどうかです。
順列とは
順列は、ABとBAという同じ組み合わせで並びが異なるものは別物として考えます。
事柄の順番にならべるの並べ方なので「順列」といいます。
【例題1】1,2,3,4の4枚のカードを使って4ケタの整数を作る時、何とおりありますか。
最初の数字を1とすると、下の図のような6とおりの組合せがあります。
最初の数字は1,2,3,4の4通りありますので、それぞれに6通りあり、
4×6=24通りとなります。
このように、順番にもれなく書き出したものを樹形図といいます。
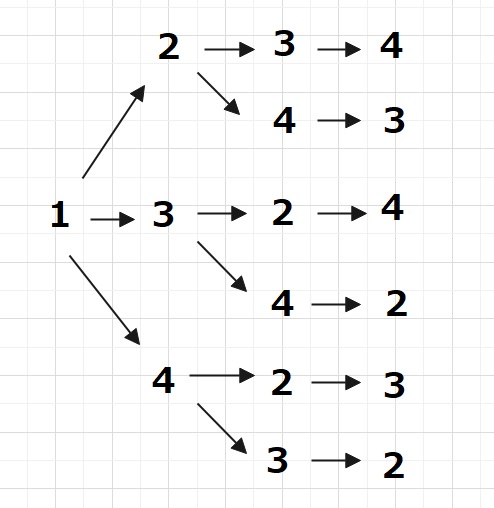
別の考え方でいくと、
千の位は 1,2,3,4の4通り考えられます。
百の位は 1つ数字を使ったので、残りの3つの数字より1つ選ぶので3通りです。
十の位は 2つ数字をつかってるので、残りの2つの数字の2通りとなります。
一の位は 1通りですね。
よって、4×3×2×1=24通りと樹形図と同じ答えとなります。
【例題2】0,1,2,3の4枚のカードを使って4ケタの整数を作る時、何通りありますか。
4ケタの整数を作るため、千の位に0は使えず、1,2,3の3通りとなります。
百の位は残りの3枚のパターンがあるので3通り、十の位は2通り、一の位は1通りとなり、
3×3×2×1=18通りとなります。
慣れるまでは樹形図でもれなく数えるほうがよいですが、なれてくると
計算することにより解答できるパターンもあります。
【例題3】0,1,2,3の4枚のカードを使って4ケタの偶数を作る時、何通りありますか。
このパターンの場合、千の位は0以外の数字、一の位は0か2という2つの縛りが
入ってきます。
このような場合は、面倒でも樹形図をかいた方が時間がかからないと思います。
下図より 4+2+4=10通り・・・(答え)となります。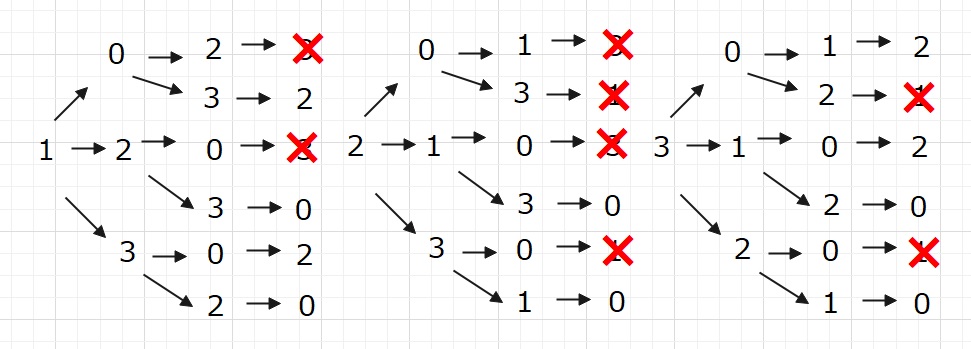
組合せとは
組合せの場合、順番は関係なくただ選ぶだけで、そのパターンが何通りあるかということです。
組合せの場合は、樹形図をかくと逆にわからなくなってしまいます。
最初に、順列(並べ方)の問題か、組合せ(選ぶだけ)の問題かを見極めることが大切です。
【例題4】A,B,C,D,E,Fの6チームが総当たりで戦う場合、何通りありますか。
図を活用する場合、下図のように多角形をイメージし、Aから順に、B、C
で組合せをかんがえていくとよいと思います。
下図より15通りとなります。
別の考え方をしてみます。まず6チームの中から2チームを並べる並べ方を
考えると、1チーム目は6通り、2チーム目は1チーム選びましたので5通りあり
6×5=30通りとなります。
しかし、ただ2チームを選ぶときABとBAは同じとかんがえますので、
30÷2=15通り同じ答えになります。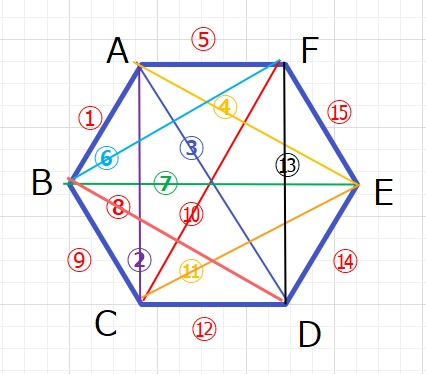
【例題5】A,B,C,D,の4人のなから3人を選ぶとき、何通りがありますか
先ほどと同じように、4人から3人を並べる並べ方を考えます。
1人目は4、2人目は3、3人目は2通りありますので4×3×2とおりあります。
しかし 3人選んだ順番は関係ないので、例えばA,B,Cが選ばれた場合、
この並べ方 3×2×1とおりは今回はダブっていることとなります。
このダブり除くと、\(\displaystyle\frac{4×3×2}{3×2}\)=4通りとなります。
実はこれ、問題の考え方を変えるともっと簡単にとけます。
「A,B,C,D,の4人のなから3人を選ぶ」とは逆をいうと、「4人の中から1人を選ばない」
ということと一緒です。ということは、4通りですね。
このように場合の数を解くときに、視点をかえて考えてみるということはとても重要です。


コメント