場合の数の問題を解くにあたり重要なことは、与えられたルールを把握して、
下記をヒントにもれなく仕分けすることです。与えられたルールをわかりやすく置き換えることも
重要なカギを握ります。
①もれなくダブりなくカウントする。
②複雑な場合は、小分けにしてグループ別に考えていく
③場合分けのパターンを少しでも減らすために、固定したり、まとめてペアにして減らしたりする
④多いパターンではなく、少ないパターンの方を数える
上記ルールでかぞえていくのですが、区別がつくか?つかないか?が重要となります。
区別がつかない場合、例えばAAB,ABA,BAAなどを同じものとみなすため、その場合
すべての場合の数を重複した場合の数でわることで場合の数を求めることができます。
【例題1】6個の異なる玉を、Aさんに 2 個、Bさんに 2個、Cさんに 2個分ける方法。
【解答】
Aさんに 2個配る場合の数 6×5 通りですが、順番は区別しない(例えば赤青と青赤は一緒とみなす)ので2×1通りダブっています。 \(\displaystyle\frac{6×5}{2×1}\)通り。
Bさんに残りの4個から2個わけると、同様に \(\displaystyle\frac{4×3}{2×1}\)通り
Cさんに残りの2個から2個分けるので1通り。
よって 15×6=90通り ・・・(答え)
【例題2】6個の異なる玉を3人に分ける方法。ただし、受け取らない人はいない。
【解答】6個の異なる玉を3人に分ける方法は3×3×3×3×3×3=729通り
2人占めのケース 2×2×2×2×2×2から1人占めのケースの2通りをひいて62通り
AB,AC,BCの3通りの2人占めのケースがあるので、62×3=186通り。
1人占めのケース 3通り。
すべての場合の数から2人占めと1人占めのケースをひいて、
729ー(186+3)=540通り・・(答え)
【例題3】6個の異なる玉を3組に分ける方法。ただし、0個の組があってよい。
【解答】すべてパターンをかきだしてみます。
①(6,0,0) 1通り
②(5,1,0) 6通り
③(4,2,0) \(\displaystyle\frac{6×5}{2×1}\)=15通り
④(4,1,1) \(\displaystyle\frac{6×5×4×3}{4×3×2×1}\)×2×1×\(\displaystyle\frac{1}{2}\)=15通り
⑤(3,3,0) \(\displaystyle\frac{6×5×4}{3×2×1}\)×\(\displaystyle\frac{1}{2}\)=10通り
⑥(3,2,1) \(\displaystyle\frac{6×5×4}{3×2×1}\)×\(\displaystyle\frac{3×2}{2×1}\)=60通り
⑦(2,2,2) \(\displaystyle\frac{6×5}{2×1}\)×\(\displaystyle\frac{4×3}{2×1}\)×\(\displaystyle\frac{1}{3×2×1}\)=15通り
よって、1+6+15+15+10+60+15=122通り・・(答え)
【例題4】6個の区別がつかない玉を、3 人に分ける方法。ただし、受け取らない人がいてもよい。
【解答】下の図の8個のポジションのどこに2個の仕切りをいれて、3つに区切るかです。
8×7×\(\displaystyle\frac{1}{2}\)=28通り 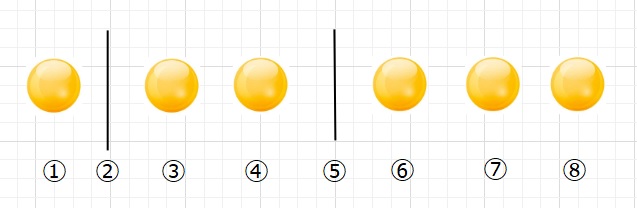
【例題5】6個の区別がつかない玉を、3人に分ける方法。ただし、全員少なくとも1つは受け取る。
【解答】
事前にA,B,Cさんに1個ずつ配っておく。
あとは5個のポジションのどこに2個の仕切りをいれるかだから、
5×4×\(\displaystyle\frac{1}{2}\)=10通り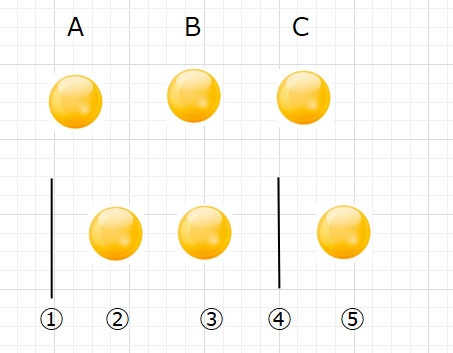
【例題6】6個の区別がつかない玉を、3組に分ける方法。ただし、0個の組があってもよい。
①(6,0,0) ②(5,1,0) ③(4,2,0) ④(4,1,1) ⑤(3,3,0) ⑥(3,2,1) ⑦(2,2,2)
7通り。・・・(答え)
コメント