難易度
女子学院中学 2022年入試問題より
1行計算問題は次の順番であわてずに処理していきます。
1.\(\frac{い}{あ}\)の入った計算問題はすべて\(\frac{い}{あ}\)にあわせます。
・小数はすべて\(\frac{い}{あ}\)に書き換えます。
・帯分数はすべて仮分数\(\frac{い}{あ}\)に書き換えます。
2.()内のたし算、ひき算は通分して\(\frac{い}{あ}\)の形にまとめます。
3.わり算 ÷\(\frac{い}{あ}\)は分母と分子をいれかえて ×\(\frac{あ}{い}\)に書き換えます。
注目するのは最初から見ていき、×÷がとぎれるところ、と()で囲われている部分です。
()内は最初に計算しておきます。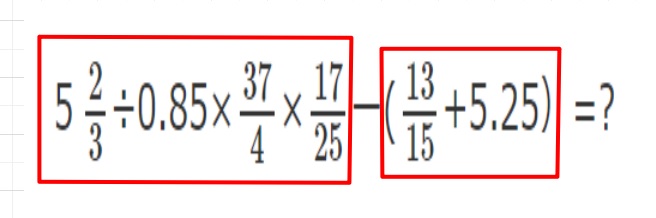
(左半分)=5\(\frac{2}{3}\)÷0.85×\(\frac{37}{4}\)×\(\frac{17}{25}\)=\(\frac{17}{3}\)×\(\frac{100}{85}\)×\(\frac{37}{4}\)×\(\frac{17}{25}\)=\(\frac{37×17}{3×5}\)
(右半分)=\(\frac{13}{15}\)+5.25=\(\frac{13}{15}\)+\(\frac{525}{100}\)=\(\frac{13}{15}\)+\(\frac{105}{20}\)=\(\frac{13}{15}\)+\(\frac{21}{4}\)=\(\frac{13×4+15×21}{5×3×4}\)=\(\frac{52+315}{5×3×4}\)=\(\frac{367}{5×3×4}\)
(与えられた式)=\(\frac{629×4-367}{5×3×4}\)=\(\frac{2149}{5×3×4}\)=\(\frac{2149}{60}\)=35\(\frac{49}{60}\)・・・(答え)
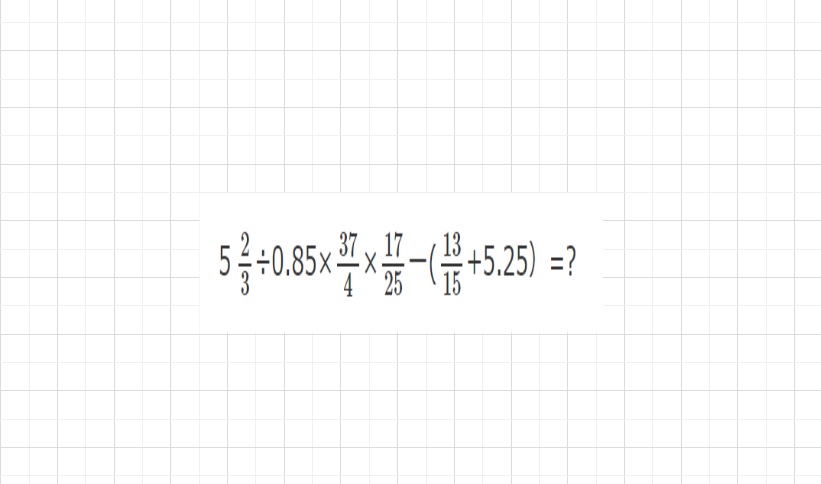


コメント