東大寺学園 2020年入試問題より
【問題】\(\frac{1}{1717}\)+\(\frac{1}{1919}\)ー\(\frac{1}{909}\)×51=(\(\frac{1}{ア}\)+\(\frac{1}{2121}\)ー\(\frac{1}{1010})\)×70 のとき、アを求めなさい。
【ヒント】1717=101×17,1919=101×19,909=101×9,2121=101×21,1010=101×10
と分解できます。
また51=3×17,70=7×10と分解できます。
1行計算問題への対応方法は、前回ご紹介した下記の通りです。今回は÷や小数はでてきません。
1.\(\frac{い}{あ}\)の入った計算問題はすべて\(\frac{い}{あ}\)にあわせます。
・小数はすべて\(\frac{い}{あ}\)に書き換えます。
・帯分数はすべて仮分数\(\frac{い}{あ}\)に書き換えます。
2.()内のたし算、ひき算は通分して\(\frac{い}{あ}\)の形にまとめます。
3.わり算 ÷\(\frac{い}{あ}\)は分母と分子をいれかえて ×\(\frac{あ}{い}\)に書き換えます。
【解答】
(左側の式)=\(\frac{1}{1717}\)+\(\frac{1}{1919}\)ー\(\frac{1}{909}\)×51
分母を1717=101×17,1919=101×19,909=101×9にそれぞれ分解します。
=\(\frac{19×9+17×9-17×19}{101×17×19×9}\)×3×17
分母を101×17×19×9で通分します。
51を3×17に分解します。
=\(\frac{9×(19+17)-17×19}{101×19×3}\)
分母の9を3×3に分解し、分子と分母の3×17を相殺(そうさい:消す)します。
分子の 19×9+17×9を9でくくり、9×(19+17)と工夫して計算します。
=\(\frac{1}{101×19×3}\)
分子の9×36-17×19を計算します。
これで左側の式がすっきりしました。
次に右側の式=(\(\frac{1}{ア}\)ー\(\frac{21-10}{101×21×10}\))×70を \(\frac{1}{ア}\)だけにするために
左側と右側に \(\frac{1}{70}\)をかけて、
さらに、\(\frac{21-10}{101×21×10}\)を両方にたします。
\(\frac{1}{ア}\)=\(\frac{1}{101×19×3}\)×\(\frac{1}{70}\)+\(\frac{21-10}{101×21×10}\)
分母を101×19×3×7×10で通分します。
=\(\frac{1+19×11}{101×19×3×7×10}\)
=\(\frac{210}{101×19×3×7×10}\)
分子の210と分母の3×7×10=210を相殺(そうさい)します。
=\(\frac{1}{101×19}\)=\(\frac{1}{1919}\)
ア=1919・・・(答え)
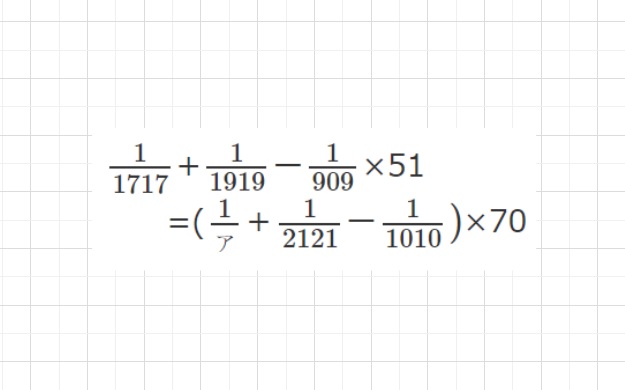


コメント