小数とは
小数(しょうすう)とは、名前のとおりで、1より小さい数を表現する数で、小数点(.)を使って表します。例えば、0.1,2.5のように表現します。
整数は、0,1,2,3,4…と続く数のことですが、整数ではそれよりも小さい数、たとえば1の「半分」などを表現することができません。それを表現するためには、「分数」をつかい「\(\frac{1}{2}\)」と表すか、小数を使い「0.5」と表現します。\(\frac{1}{2}\)と0.5は同じ数をさし、分数は小数で表現することができます。
しかし、小数は分数で表現できるとは限りません。(のちほど紹介します。)
小数の種類
小数には大きく分けて3つの種類に分けることができます。
1 .有限小数 0.125や4.3792のように小数点以下が有限なものをいいます。
0.125は
小数点第1位(10分の1の位) 0.1を1個
小数点第2位(100分の1の位) 0.01を2個
小数点第3位(1000分の1の位) 0.001を5個 集めた数を表します。
2.無限小数 小数点以下の数が不規則で無限につづく小数(これは無理数とよばれています)
代表的なものに、円周率 π(パイ)があり、3.14159265…のように小数点以下の数が不規則で無限につづきます。この小数は分数で表せない数でもあります。
3.循環小数・・・小数点以下の数が無限に続く数(無限小数)のなかでも数が循環する小数
例)0.333・・・や 0.48123123123・・・
この数は、0.333・・・=\(\frac{1}{3}\)のように分数で表すことができます。
詳しくは別の機会にお話しします。
小数の計算
1.小数のたし算・ひき算
小数点の位置をあわせて、各くらいどうしを計算していきます。
たとえば、 0.123+35.2 を計算するとき
整数部分 0+35=35
小数第1位 1+2=3 小数第2位 2+0=2 小数第3位 3+0=3となり
35.323と計算できます。仕組みを書くと複雑に見えますが、下のようにひっ算で書くと
わかりやすいと思います。くり上がりがある場合も、普通のたし算どうように数字をくりあげます。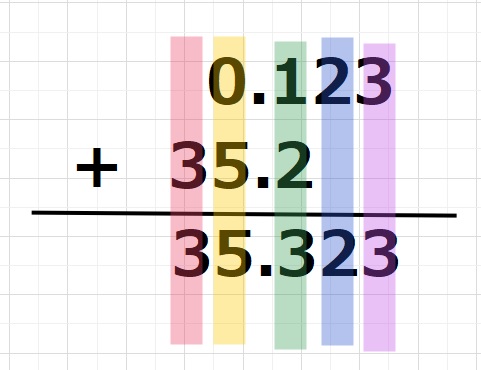
2.小数のかけ算とわり算
小数のかけ算とわり算は、小数点の位置をずらし、どちらも整数にしてまず計算します。
そして最後にずらした小数点の数だけ戻すようにします。
たとえば、0.123×35.2を計算する場合、123×352を計算しますが、
小数点の位置を 0.123は3個右にずらし、35.2は1個右にずらしています。
そのため、計算した数字からさいごに逆に合計4個左へずらしたところに小数点をうちます。
理屈は 0.123×\(\frac{1000}{1000}\)×35.2×\(\frac{10}{10}\)=123×352×\(\frac{1}{10000}\)ということです。
これが、123×352を計算し、\(\frac{1}{10000}\)倍つまり、小数点を左に4つずらすということになります。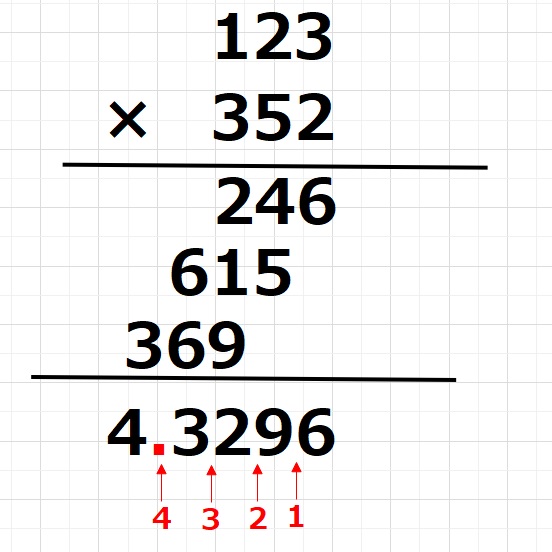
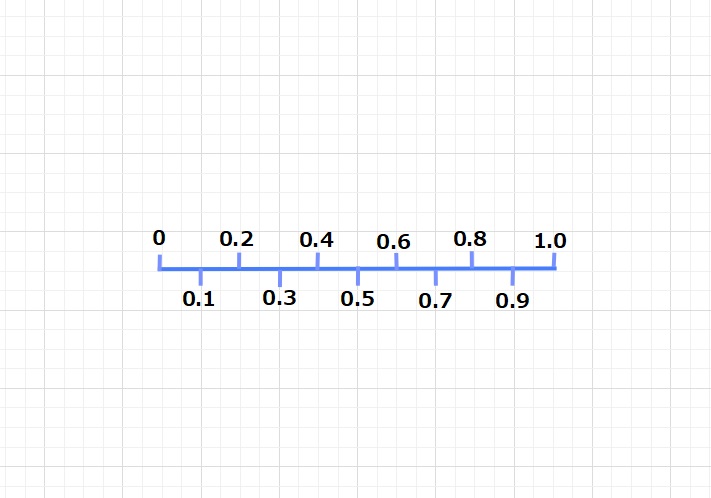

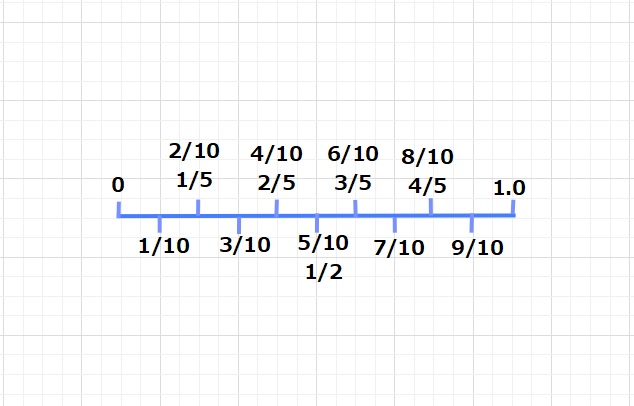
コメント